第八章 无序定律
一、热的无序
斟上一杯水,并且仔细观察它,这时,你看到的只是一杯清澈
而均匀的液体,看不出有任何内部运动的迹象(当然,这是指不
晃动玻璃杯而言)。但我们知道,水的这种均匀性只是一种表面现
象。如果把水放大几百万倍,就会看出它具有明显的颗粒结构,是
由大量紧紧地挨在一起的单个分子组成的。
在这样的放大倍数下,我们还可以清清楚楚地看到,这杯水
绝非处于静止状态。它的分子处在猛烈的骚动中,它们来回运动。
互相推挤。恰似一个极度激动的人群。水分子或其他一切物质分
子的这种无规运动叫做热运动,因为热现象就是这种运动的直接
结果。尽管肉眼不能察觉到分子和分子的运动,但分子的运动能
对人体器官的神经纤维产生一定的刺激,从而使人产生热的感觉。
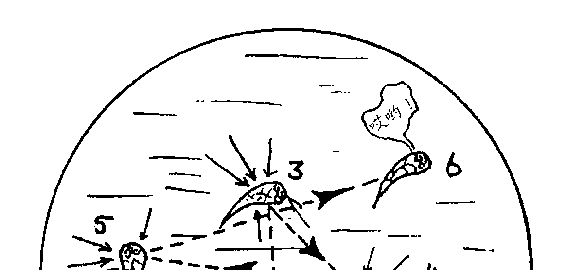
对于比人小得多的生物,如悬浮在水滴中的细菌,这种热运动的
效应就要显著得多了。这些可怜的细菌会被进行热运动的分子从
四面八方无休止地推来搡去,得不到安宁(图 77)。这种可笑的现
象是 100 多年前英国生物学家布朗(Robert Brown)在研究植物花
粉时首次发现的,因此被称为布朗运动。这是一种普遍存在的运
动,可在悬浮在任何一种液体中的任何一种物质微粒(只要它足
够细小)上观察到,也可以在空气中飘浮的烟雾和尘埃上观察到。
如果把液体加热,那么,悬浮小微粒的狂热舞蹈将变得更为
奔放;如果液体冷却下来,舞步就会显著变慢。毫无疑问,我们所
观察到的现象正是物质内部热运动的效应。因此,我们通常所说
的温度不是别的,而正是分子运动激烈程度的量度。通过对布朗
161
20&世纪科普经典特藏 从一到无穷大
图 77 一个细菌被周围分子推来搡去而连续换了六个位置
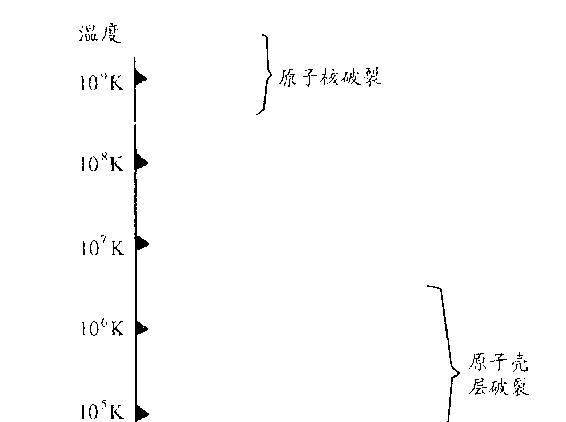
运动与温度的关系进行研究,人们发现在温度达到-273℃,即
-459℉时,物质的热运动就完全停止了。这时,一切分子都归于
静止。这显然就是最低的温度。它被称为绝对零度。如果有人提起
更低的温度,那显然是荒唐的。因为哪里会有比绝对静止更慢的
运动呢?
一切物质的分子在接近绝对零度这个温度时,能量都是很小
的。因此,分子之间的内聚力将把它们凝聚成固态的硬块。这些分
子只能在凝结状态下作轻微的颤动。如果温度升高,这种颤动就
会越来越强烈;到了一定程度,这些分子就可以获得一定程度的
运动自由,从而能够滑动。这时,原先在凝结状态下所具有的硬度
消失了,物质就变成了液体。物质的溶解温度取决于分子内聚力
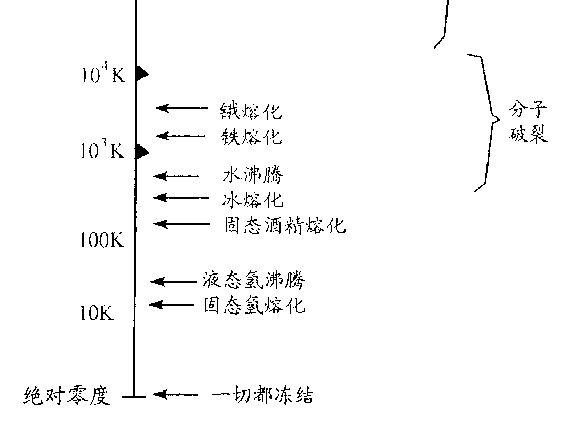
的强度。有些物质,如氢或空气(氮和氧的混合物),它们分子间
的内聚力很微弱,在很低的温度下就会被热运动所克服。氢要到
14K(即-259℃)下才处于固体状态,氧和氮则分别在 55K 和
64K(即-218℃和-209℃)时熔解。另一些物质的分子则有较强
的内聚力,因此能在较高温度下保持固态。例如,酒精能保持固态
162
第八章 无 序 定 律
到-114℃,固态水(即冰)在 0℃时才融化。还有一些物质能在
更高的温度下保持固态:铅在+327℃熔解,铁在+1535℃,而稀
有金属锇能坚持到+2700℃。物质在处于固态时,它们的分子显然
是被紧紧束缚在一定的位置上,但绝不是不受热的影响。根据热
运动的基本定律,处在相同温度下的一切物质,无论是固体、液体
还是气体。其单个分子所具有的能量是相同的,只不过对某些物
质来说,这样大的能量已足以使它们的分子从固定位置上挣脱开
来,而对另一些物质来说,分子只能在原位上振动,如同被短链子
拴住的狂怒的狗一样。
固体分子的这种热颤动或热振动,在上一章所描述的 X 光照
片中可以很容易地观察到。我们确实知道,摄得一张晶格分子的
照片需要一定时间,因此在这段曝光时间内,绝对不能允许分子
离开自己的固定位置。来回颤动非但无助于拍照,反而会使照片
模糊起来。这种模糊现象可从图版Ⅰ那张分子照片上看到。为了
得到清晰的图像,必须尽可能把晶体冷却,这一般是把晶体浸到
液态空气中来实现的。反过来,如果把被摄影的晶体加热,照片就
会变得越来越模糊。当达到熔点时,由于分子脱离原来的位置,在
熔解的液体里无规地运动起来,它的影像就会完全消失。
在固体熔化后,分子仍然会聚在一起。因为热冲击虽然已大
得能把分子从晶格上拉下来,却还不足以使它们完全离开。然而,
当温度进一步升高时,分子间的内聚力就再也不能把分子聚拢在
一起了。这时,如果没有容器壁的阻挡,它们将沿各个方向四散飞
开。这样一来,物质当然就处在气态了。液体的气化也和固体的熔
化一样,不同的物质有不同的温度;内聚力弱的物质变成气体所
需达到的温度要比内聚力强的物质低。汽化温度还与液体所受压
力的大小有重大关系,因为外界的压力显然是会帮内聚力的忙的。
我们知道,正因为如此,封得很严实的一壶水,它的沸腾温度要比
在敞开时高;另一方面,在大气压大为减低的高山项上,水不到
100℃就会沸腾。顺便提一下,测量水在某个位置上的沸腾温度,
163

20&世纪科普经典特藏 从一到无穷大
图 78
就可以计算出大气压强,也就可以知道这个位置的海拔高度。
但是,可不要学马克·吐温&*(Mark Twain)所说的那个例子
* 马克·吐温是著名的美国作家。在他的《漫游外国记》中,有这样一则幽默故事:
几个去阿尔卑斯山远足的人,想测量一下山的高度。这本来可以由气压计的读数计算出来,
也可测量水的沸点而推得。但他们却记成应该把气压计放到沸水里煮一下,结果把气压计
煮坏了,没能读出数来,而煮过气压计的水用来做菜汤时,味道竟很好。——译者
164
第八章 无 序 定 律
啊!他在一篇故事里讲到,他曾把一支无液气压计放到煮碗豆汤
的锅子里。这样做非但根本不能判断出任何高度,这锅汤的滋味还
会被气压计上的铜氧化物弄坏。
一种物质的熔点越高,它的沸点也越高。液态氢在-253℃沸
腾。液态氧和液态氮分别在-183℃和-196℃,酒精在+78℃,铅
在+162℃,铁在+3000℃,锇要到+5300℃①。
在固体那美妙的晶体结构被破坏以后,它的分子先是像一堆
蛆虫一样爬来爬去,继而又像一群受惊的鸟一样飞散开。但这并
不是说,热运动的破坏力已达到极限。如果温度再行升高就会威
胁到分子本身的存在,因为,这时候分子间的相互碰撞变得极为猛
烈,有可能把分子撞开成为单个原子。这种被称为热离解的过程
取决于分子的强度;某些有机物质在几百度时就会变为单个原子
或原子群,另一些分子可要坚牢的多,如水分子它要到 1000 度
以上才会崩溃。不过,当温度达到几千度时,分子就不复存在了,
整个世界就将是纯化学元素的气态混和物。
在太阳的表面上,情况就会是这样,因为这里的温度可达
6000℃。而在比太阳“冷”一些的红巨星&②的大气层中,就能存在
一些分子,这已经靠专门的分析方法得到了证实。
在高温下,猛烈的热碰撞不仅把分子分解成原子,还能把原
子本身的外层电子去掉,这叫做热电离。如果达到几万度、几十万
度、几百万度这样的极高温度——这样的温度超过了实验室中所
能获得的最高温度,然而在包括太阳在内的恒星中却是屡见不鲜
的——热电离就会越来越占优势。最后,原子也完全不能存在了,
所有的电子层都统统被剥去,物质就只是一群光秃秃的原子核和
自由电子的混合物。它们将在空间中狂奔猛撞。尽管原子个体遭
到这样彻底的破坏,但只要原子核完好无缺,物质的基本化学特
性就不会改变。一旦温度下降,原子核就会重新拉回自己的电子,
① 这里的所有数值都是在标准大气压下测得的。
② 见第十一章。
165
20&世纪科普经典特藏 从一到无穷大
完整的原子又形成了。
为了达到物质的彻底热裂解,使原子核分解为单独的核子
(质子和中子),温度至少要上升到几十亿度。这样高的温度,目
前即使在最热的恒星内部也未发现。也许在几十亿年以前,我们
这个宇宙正当年轻时曾有过这种温度。这个令人感兴趣的问题,
我们将在本书最后一章加以讨论。
这样,我们看到,热冲击的结果使得按量子力学定律构筑起
来的精巧物质结构逐步被破坏,并把这座宏大建筑物变成乱糟糟
的一群乱冲瞎撞看不出任何明显规律的粒子。
图 79 温度的摧毁效应
166
第八章 无 序 定 律
二、如何描述无序运动?
如果你认为,既然热运动是无规则的,所以就无法对它进行
任何物理描述,那可就大错而特错了。对于完全不规则的热运动,
有一类叫做无序定律、或者更经常被称做统计定律的新定律在起
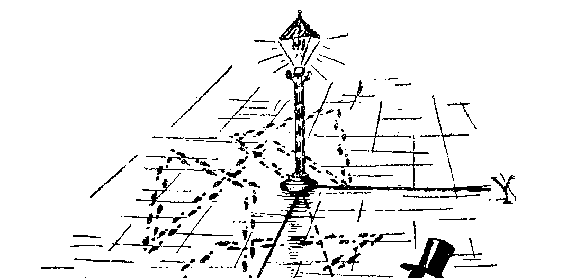
作用。为了理解这一点。让我们先来注意一下著名的“醉鬼走路”
问题。假设在某个广场的某个灯柱上靠着一个醉鬼(天晓得他在
什么时侯和怎么跑到这儿来的),他突然打算随便走动一下。让我
们来观察他的行动吧。他开始走了:先朝一个方向走上几步,然后
换个方向再迈上几步,如此这般,每走几步就随意折个方向(图
80)。那么,这位仁兄在这样弯弯折折地走了一段路程,比如折了
100 次以后,他离灯柱有多远呢?乍一看来,由于对每一次拐弯的
情况都不能事先加以估计,这个问题似乎是无法解答的。然而,仔
细考虑一下,就会发觉,尽管我们不能说出这个醉鬼在走完一定
路程后肯定位于何处,但我们还是能答出他在走完了相当多的路
程后距离灯柱的最可能的距离有多远。现在,我们就用严格的数
学方法来解答这道题目。以广场上的灯柱为原点画两条坐标轴,&X
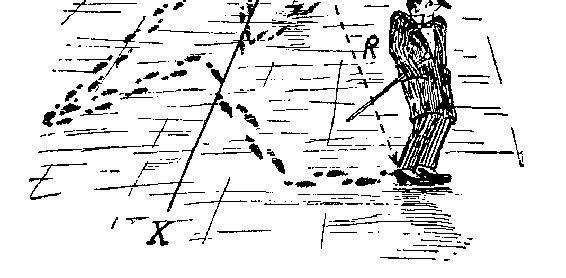
轴指向我们,&Y&轴指向右方。&R&表示醉鬼走过&N&个转折后(图 80
中&N&为 14)与灯柱的距离。若&Xn&和&Yn&分别表示醉鬼所走路径的
第&N&个分段在相应两轴上的投影,由毕达哥拉斯定理显然可得出:
R&2 = (&X&1&+&X&2&+&X&3&+ … +&Xn)2 +
(&Y&1&+&Y&2&+&Y&3&+ … +&Yn)2,
这里的&X&和&Y&既有正数,又有负数,视这位醉鬼在各段具体路程
中是离开还是接近灯柱而定。应该注意,既然他的运动是完全无
序的,因此在&X&和&Y&的取值中,正数和负数的个数应该差不多相
等。我们现在按照代数学的基本规则展开上式中的括号,即把括
号中的每一项都与自己这一括号中的所有各项(包括自己在内)
相乘。这样,
(&X&1 +&X&2 +&X&3 + … +&Xn)2
167
20&世纪科普经典特藏 从一到无穷大
图 80 醉鬼所走的路
=(&X&1 +&X&2 +&X&3 + … +&Xn)(&X&1 +&X&2 +&X&3 + … +&Xn)
=&X&2
2
2
1 +&X&1&X&2 +&X&1&X&3 + … +&X&2 +&X&1&X&2 + … +&Xn&这一长串数字包括了&X&的所有平方项(&X&2
2
2
1 ,&X&2 ,…&Xn&)和所谓
“混和积”,如&X&1&X&2,&X&2&X&3 等等。
到目前为止,我们所用到的只不过是简单的数学。现在要用
到统计学观点了。由于醉鬼走路是无规则的,他朝灯柱走和背着
灯柱走的可能性相等,因此在&X&的各个取值中,正负会各占一半。
这样,在那些“混和积”里,总是可以找出数值相等、符号相反
的一对对可以互相抵消的数对来;&N&的数目越大,这种抵消就越彻
底。只有那些平方项永远是正数,因而能够保留下来。这样,总的
结果就变成
X&2
2
2
1 +&X&2 + … +&Xn&=&NX&2,
168
第八章 无 序 定 律
X在这里表示各段路程在&X轴上投影长度的平均值&*。
同理,第二个括号也能化为&NY&2,&Y&是各段路程在&Y&轴上投影
长度的平均值。这里还得再说一遍,我们所进行的并不是严格的
数学运算,而是利用了统计规律,即考虑到由于运动的任意性所
产生的可抵消的“混和积”。现在,我们得到醉汉离开灯柱的可能
距离为
2 = ( 2
2
R
N X&+&Y&)
或
2
2
R&=&N&·&X&+&Y
但是各路程的平均投影在两根轴上都是 45°,所以
2
2
X&+&Y
就等于平均路程长度(还是由毕达哥拉斯定理证得)。用 1 来表示
这个平均路程长度时,可得到
R&= 1⋅&N&。
用通俗的语言来说,这就是:醉鬼在走了许多段不规则的曲折路
程后,距灯柱的最可能距离为各段路径的平均长度乘以路径段数
的平方根。
因此,如果这个醉鬼每走一米就(以随意角度)拐一个弯,
那么,在他走了 100 米的长路后,他距灯柱的距离一般只有 10 米;
如果笔直地走呢,就能走 100 米——这表明,走路时有清醒的头脑
肯定会占很大便宜的。
从上面这个例子可以看出统计规律的本质:我们给出的并不
是每一种场合下的精确距离,而是最可能的距离。如果有一个醉
鬼偏偏能够笔直走路不拐弯(尽管这种醉鬼是太罕见了),他就会
沿直线离开灯柱。要是有另一个醉鬼每次都转 180°的弯,他就会
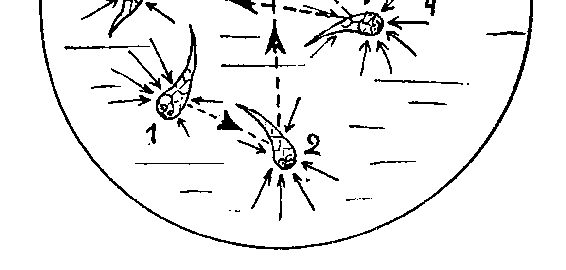
离开灯柱又折回去。但是,如果有一大群醉鬼都从同一根灯柱开
始互不干扰地走自己的弯弯路,那么,经过一段足够长的时间后,
你将发现他们会按上述规律分布在灯柱四周的广场上。图 81 画出
* 严格地说是方均根值,即平方的平均数再开平方。——译者
169
20&世纪科普经典特藏 从一到无穷大
了六个醉汉无规则走动时的分布情况。不消说,醉汉越多、不规则
弯折的次数越多,上述规律也就越精确。
图 81 灯柱附近六名醉鬼的统计分布情况
现在,把一群醉鬼换成一批很小的物体,如悬浮在液体中的
植物花粉或细菌,你就会看到生物学家布朗在显微镜下看到的那
种现象。当然,花粉和细菌是不喝酒的,但我们曾说过,它们被卷
入了周围分子的热运动,被它们不停地踢向各个方向,因此被迫
走出弯弯曲曲的路,恰像那因酒精作怪而失去了方向概念的人
一样。
在用显微镜观看悬浮在一滴水中的许多小微粒的布朗运动时,
你可以集中精力观察在某个时刻位于同一小区域内(靠近“灯
柱”)的一批微粒。你会发现,随着时间的推移,它们会逐渐分散
到视场中的各个地方,而且它们与原来位置的距离同时间的平方
根成正比,正如我们在推导醉鬼公式时所得到的数学公式一样。
这条定律当然也适用于水滴中的每一个分子。但是,人们是
看不见单个分子的,即使看见了,也无法将它们互相区别开。因
此,我们得采用两种不同的分子,凭借它们的不同(如颜色)而
看出它们的运动来。现在,我们拿一个试管,注入一半呈漂亮紫色
170
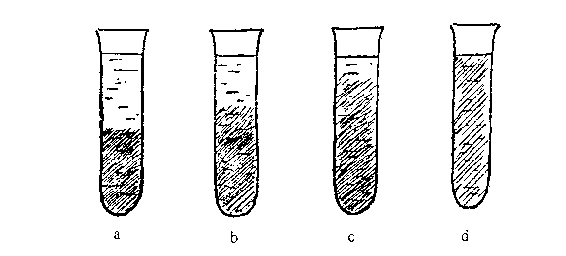
第八章 无 序 定 律
的高锰酸钾水溶液,再小心地注入一些清水,同时注意不要把这
两层液体搞混。观察这个试管。我们就会看到,紫色将渐渐进入清
水中去。如果观察足够长的时间,全部液体就会从底部到顶那都
变成颜色均匀的统一体(图 82)。这种为大家所熟知的现象叫做扩
散。它是高锰酸钾染料的分子在水中的无规则热运动所引起的。
我们应该把每个高锰酸钾分子想像成一个小醉鬼,被周围的分子
不停地冲来撞去。水的分子彼此挨得很近(与气体分子相比),因
此,两次连续碰撞间的平均自由程很短,大约只有亿分之一英寸。
另一方面,分子在室温下的速度大约为 1/10 英里每秒,因此,一
个分子每隔一万亿分之一秒就会发生一次碰撞。这样,每经过 1 秒
钟,1 个单个染料分子发生碰撞并折换方向的次数达上万亿次,它
在 1 秒钟内走出的距离就是亿分之一英寸(平均自由程)乘以 1
万亿的平方根,即每秒钟走出 1%英寸。这就是扩散的速度。考虑
到在没有碰撞时分子在 1 秒钟后就会跑到 1/10 英里以外的地方去,
可见,这种扩散速度是很慢的。要等上 100 秒钟,分子才会挪到
10 倍( 100 = 10 )远的地方;要经过 10 000 秒钟,也就是将近 3
个小时,颜色才会扩展 100 倍( 10000 = 100 )即 1 英寸远。
瞧,扩散可是个相当慢的过程啊。所以,如果你往茶里放糖&*,还
是要用匙搅动搅动,不要干等糖分子自行运动到各处去。
图 82
* 欧美人饮茶的习惯是加糖的。——译者
171
20&世纪科普经典特藏 从一到无穷大
我们再来看一个扩散的例子:热在火炉通条中的传导方式,
这是分子物理学中最重要的过程之一。把一根铁通条的一端插入
火中,根据经验可知,另一端要在相当长的时间之后才会变得烫
手。你大概并不知道这热量是靠电子的扩散传递过来的。火炉通
条也好,其他各种金属也好,内部都有许多电子。这些电子和诸如
玻璃之类的非金属物质中的电子不同,金属中那些位于外电子壳
层的电子能够脱离原子,在金属晶格内游荡。它们会像气体中的
微粒一样参与不规则热运动。
金属物质的外表面层是会对电子施加作用力、不让它们逃出
的&①;但在金属内部,电子却几乎可以随意运动。如果给金属线加
上一个电场作用力,这些不受约束的自由电子将沿电场作用力的
方向冲过去,形成电流;而非金属物质的电子则被束缚在原子上,
不能自由运动,因此,非金属大都是良好的绝缘体。
当把金属棒的一端插入火中,这一部分金属中自由电子的热
运动便大为加剧;于是这些高速运动的电子就开始携带过多的
热能向其他地区扩散。这个过程很像染料分子在水中扩散的情况,
只不过这里不是两种不同的微粒(水分子和染料分子),而是热电
子气扩散到冷电子气的区域中去。醉鬼走路的定律在这里也同样
适用,热在金属棒中传递的距离与相应时间的平方根成正比。
最后,再举一个与前二者截然不同而具有宇宙意义的重要扩
散例子。在下一章中,我们将看到,太阳的能量是由它自己内部深
处的元素在嬗变时产生的。这些能量以强辐射的形式释放出去。
这些“光微粒”,或者说光量子,从太阳内部向表面运动。光的速
度为 300 000 公里每秒,太阳的半径为 700 000 公里。所以,如果
光量子走直线的话,只消 2 秒多钟就会从中心到达表面。但事实上
绝非如此。光量子在向外行进时,要与太阳内部无数的原子和电
子相撞。光量子在太阳内的自由程约为 1 厘米(比分子的自由程
① 当金属丝处在高温状态时,它内部电子的热运动将变得足够猛烈,使得一些电子从
表面射出。这现象已被用于电子管,这是无线电爱好者所熟知的事实。
172
第八章 无 序 定 律
长多了!),太阳的半径是 70 000 000 000 厘米,这样,光量子就得
像醉汉那样拐上 (7×l010)2 即 5×1021 个弯才能到达表面。这样,
每一段路需要花
1
即 3×10-11 秒,而整个旅程所用的时间即
10
3×10
为 3×l0-11×5×l021=1.5×l011 秒,也就是 5000 年上下!这一回,
我们又一次看到扩散过程是何等缓慢。光从太阳中心走到表面要
花 50 个世纪。而从太阳表面穿越星际空间直线到达地球,却仅仅
用 8 分钟就够了。
三、计算概率
上面关于扩散的讨论只是把概率的统计定律应用于分子运动
的一个简单例子。在进行深入一步的讨论,以了解最重要的熵的
定律这个总辖一切物体——小到一滴液体,大到由恒星组成的宇
宙——的热行为的定律之前,我们先得学习一点计算各种简单和
复杂事件的可能性(即概率)的方法。
最简单的概率问题莫过于掷钱币了。人人都知道,掷出的硬
币正面朝上和反面朝上的概率是相等的(如果不作弊的话)。我们
把这种出现正面和反面的可能性称为一半对一半的机会。如果把
1 1
得正面的机会和得反面的机会相加,就得到 + = 1 。在概率理
2 2
论中,整数 1 意味着必然性。在掷钱币时,不是可以肯定地判断
说,不得正面则必得反面吗?!当然,如果硬币滚到床下,再也找
不到了,这又另当别论。
假如现在把一枚钱币接连掷两次,或者同时掷两枚钱币(这
两种情况是一样的),那么不难看出,会有图 83 所示的四种不同的
可能性。
第一种情形是得到两个正面,最后一种情形是两个反面。中
间的两种情形实际上是同一种,因为先是正面或先是反面(或哪
枚正面,哪枚反面),这是无所谓的。这样,我们可以说,得两个
173
20&世纪科普经典特藏 从一到无穷大
图 83 掷两枚硬币的四种可能性
正面的机会是 1:4,即 1 ,得两个反面的机会也是 1 ,得一正一反
4
4
的机会是 2:4,即 1 。 1 1 1
+ + = 1。这就是说,每掷一次,三种
2
4 4 2
情况必定出现一种。再来看看掷三个钱币的情况,可能性概括起
来如下表
第一枚 正 正 正 正 反 反 反 反
第二枚 正 正 反 反 正 正 反 反
第三枚 正 反 正 反 正 反 正 反
Ⅰ Ⅱ Ⅱ Ⅲ Ⅱ Ⅱ Ⅲ Ⅳ
从这张表中可以看出得三枚都是正面的机会为 1 ,得三枚都是反面
8
的机会也为 1 。其余的可能性被两正一反和两反一正两种情况均
8
分,各得 3 。
8
这种表的篇幅增长得很快,不过,我们还是可以看一看在掷 4
枚钱币时的情况。这时有如下 16 种可能性:
第一枚 正 正 正 正 正 正 正 正 反 反 反 反 反 反 反 反
第二枚 正 正 正 正 反 反 反 反 正 正 正 正 反 反 反 反
174
第八章 无 序 定 律
第二枚 正 正 反 反 正 正 反 反 正 正 反 反 正 正 反 反
第四枚 正 反 正 反 正 反 正 反 正 反 正 反 正 反 正 反
Ⅰ Ⅱ Ⅱ Ⅲ Ⅱ Ⅲ Ⅲ Ⅳ Ⅱ Ⅲ Ⅲ Ⅳ Ⅲ Ⅳ Ⅳ Ⅴ
1
在这里,得到四个正面的概率为
,得到四个反面的概率也是
16
4
1
一样。三正一反和三反一正都各有
即 的概率,正反相等的情况
16
4
6
3
的概率为
,即 。
16
8
照这种方式列下去,掷的枚数一多,表就会长得把你的纸用
光都写不下。例如,掷十枚时,就会有 1024 种可能性(即 2×2
×2×2×2×2×2×2×2×2)。不过,我们根本不需要罗列这些长
表格,只要从前面列过的这几张简单情况的表中,就可以观察出
判断概率大小的简单法则,并把它直接运用到较复杂的情况中去。
首先,我们看到,掷两次时得两个正面的概率等于第一和第
二中分别得到正面的概率之乘积,具体说来就是
1
1 1
= × 。
4
2 2
同样,连得三个正面和连得四个正面的概率也为每次扔掷中得到
正面的概率的乘积
1
1 1 1
1
1 1 1 1
= × ×
;
= × × × 。
8
2 2 2
16
2 2 2 2
因此,若有人问起连掷 10 次都得到正面的机会有多大,你可以不
1
费力气地把 自乘 10 次的得数告诉他。这个数是 0.00098。它表明
2
出现这种情况的可能性很小,大概只有千分之一的机会!这就是
“概率相乘”的法则。具体地说,如果你需要同时得到几个不同的
事件,你可以把单独实现每一个事件的概率相乘来得到总的概率。
假若你需要不少事件,而每一个事件又都不是那么有把握实现的
话那么,你希望它们全部实现的机会实在是小得令人沮丧啊!
另外,还有一个法则,即“概率相加”法则,内容是:如果
175
20&世纪科普经典特藏 从一到无穷大
你需要几个事件当中的一个(无论哪一个都行),这个概率就等于
所需要的各个事件单独实现的概率之和&*。
这条法则在掷钱两次、正反各一的那个例子中表现得很明
白:你所需要的或者是“先正后反”,或者是“先反后正”,这两
1
个事件,每个单独实现的概率都为 ,因此得到其中任何一个的概
4
1 1
1
率为 + = 。总之,如果你要求的是“又有某事,又有某事,
4 4
2
还有某事,……”的概率,就应把各事单独实现的概率相乘;如
果你要求的是“或者某事,或者某事、或者某事,……”的概率,
就应把各个概率相加。
在前一种、即什么都打算要的情况下,要的事件越多,实现的
可能性越小;在后一种、即只要其中某一事件的情况下,供选择的
名单越长,得到满足的可能性越大。
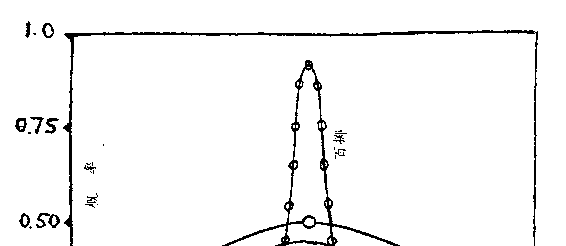
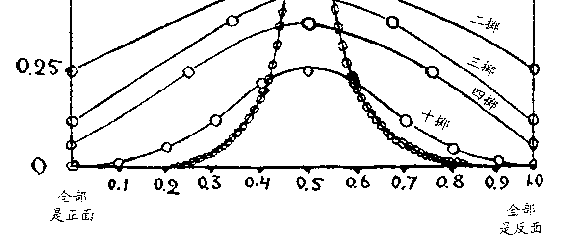
当实验的次数很多时,概率定律就变得很精确了。掷钱币的
实验就很好地证明了这一点。图 84 给出了扔掷 2 次、3 次、4 次、
10 次和 100 次钱币时,得到不同正、反面分布的概率。可以看出,
掷的次数越多,概率曲线就变得越尖锐,正、反面以一半对一半的
机会出现的极大值也就越突出。
因此,在掷 2 次、3 次以至 4 次的情况下,统统是正面或反面
的机会还是相当可观的。在掷 10 次的情况下,即使是 90%是正面或
反面的机会都很难出现。如果次数更多,例如掷 100 或 1000 次,
概率曲线会尖得像一根针,即使从一半对一半的分布上稍稍偏离
一点点,在实际上也是不可能出现的。
现在我们用刚刚学过的概率计算的简单法则,来判断在一种
有名的扑克牌游戏中,五张牌表现出各种组合的可能性。
也许你还不会玩这种牌戏,所以我现在来简单说明一下:参
加者每人摸五张牌,以得到最好的组合牌型者为赢家。这里我们
* 这条法则只适用于各个事件都不相容的情况。——译者
176
第八章 无 序 定 律
图 84 得到正、反面的相对次数
略去了为凑成一手好牌而交换几张牌所引起的附加的复杂化,也
不讨论靠诈术给对方造成你得到了好牌的错觉而自动认输的心理
学战略——其实诈术才是这种牌戏的核心所在,并使得著名丹麦
物理学家玻尔设计了一种全新的玩法:根本无须用牌,参加者只
消谈出自己想像中的组合,并互相蒙诈就行。这已全然超出概率
计算的范围,成了纯心理学的问题了。
现在让我们计算一下扑克牌中某些组合的概率来作为练习。
有一种组合叫做“同花”,即五张牌都属于同一花色(图 85)。
如果想要摸到一副同花,第一张是什么牌是无所谓的。只要
计算另外 4 张也和第一张属于同一花色的概率就行了。一副牌共
52 张,每一花色 13 张&①。在你摸去第一张以后,这种花色就只剩
12
下了 12 张。因此,第二张也属于这一花色的机会为
。同样,第
51
① 此处省去了 52 张牌以外的、可代替任意一张牌的“百搭”所引起的复杂变化。
177


20&世纪科普经典特藏 从一到无穷大
11
10
9
三、第四、第五张依然属于同一花色的可能性分别为
、
、
,
50
49
48
既然我们要求所有 5 张都同一花色,就要用概率乘法。这样,你会
发现,得到同花的概率为:
12 11 10
9
11880
1
×
×
×
=
≈
。
51 50 49 48
5997600
500
但是,不要以为每玩 500 次,一定会得到 1 次同花。你可能一
次也摸不到,也可能摸到两次。我们这里仅仅是在计算可能性。有
可能,你连摸 500 多次,1 次同花也摸不到;也可能恰恰相反。你
第 1 次就摸来个同花。概率论所能告诉你的只是在 500 次游戏中,
可能碰到 1 次同花。用同样方法你可以计算出,在 3 千万次游戏中,
可能有 10 次得到 5 张爱司(包括“百搭”在内)的机会。
另一种更为少见、因而也就更为宝贵的组合就是所谓“福尔
豪斯”&*又称为“三头两只”。它包括一个“对”和一个“对半”
(即有两张牌同一点数,另外三张为相同的另一点数。如图 86 所示
的两张 5、三张Q)。
图 85 同花(黑桃) 图 86 三头两只(福尔豪斯)
做成三头两只时,头两张牌为什么点数是无所谓的,但在后 3
张中,则应有两张与前面两张之一的点数相同,第三张与前两张中
的另一张点数相同。因为还剩下六张牌(如果已摸到一张 5、一张
Q,那就还剩下 3 张 5 和 3 张 Q)可供组合,所以第三张合乎要求
* 英文 full house 的译音。这正是这种牌戏的名称。——译者
178
第八章 无 序 定 律
6
的概率是
。在剩余的 49 张牌中还有 5 张合格的牌,所以第四张
50
5
4
也满足条件的概率为
。第五张也合格的概率为
。因此,得到三
49
48
头两只的概率为
6
5
4
120
×
×
=
。
50 49 48 117600
这差不多是同花概率的一半&*。
同样,我们还能算出其他组合如“顺子”
(即点数连续的五张
牌)等的概率,以及算出包括“百搭”在内和进行交换所表现的概
率来。
通过这种计算可以看出,扑克牌中一副牌的好坏级别正是与
它的数学概率值相对应的。这究竟是由过去某个数学家所安排的
呢,还是靠聚集在全世界的各个豪华或破烂赌窟里的数以百万计
的赌棍们拿钱财冒险而从经验中得出来的呢?我们不得而知。如果
是源于后者的话,我们可得承认,对于研究复杂事件的相对概率
来说,这确是一份非常突出的统计材料!
另一个有趣而出乎意料的概率计算的例子是所谓“生日重合”
的问题。请回忆一下,你是否曾在同一天接到过两份生日晚会的
请柬。你可能要说这种可能性很小,因为你大概只有 24 个朋友会
邀请你参加他们的生日晚会,而一年却有 365 天呢!既是有这么多
天数供选择,因此,你的 24 个朋友中,两个人在同一天吃生日蛋
糕的机会一定是非常之小吧。
然而,你的判断是大错特错的。尽管听起来似乎不能令人置
信,但实际情况却是:24 个人当中,有两个人、甚至几组两个人
* 实际上概率还要小一些,因为上述计算中还包括了“四头一只”
(姑且让我们这样来
称呼四张同点牌加其他任意一张的情况)。这种概率为
⎛ 3
2
1 ⎞
12
2×
×
×
=
⎜
⎟
。
⎝ 50 49 48 ⎠ 117600
减去这个数值后,得到三头两只的概率为
120 −12
108
=
——译者
。
117600
117600
179
20&世纪科普经典特藏 从一到无穷大
的生日相重合的概率是相当高的,实际上要比不出现相合的概率
还要大。
要想证实这一点。你可以列出一张 24 个人的生日表来,或干
脆从《美国名人录》之类的书上任选一页,随意点出 24 个人来查查
看。当然,我们也可以运用在掷钱币和玩扑克牌这两个题目上
早已熟悉了的简单概率法则,来算算这道题目的概率
我们先来计算 24 个人生日各不相同的概率。先看第一个人,
他的生日当然可以是一年中的任意一天。那么,第二个人与第一
个人不是同一天生日的可能性有多大呢?这个人(第二个)可能
出生于任何一天,因此,在 365 个机会中有一个与第一个人相重
364
合,有 364 个不相重合(即概率为
)。同样,第三个人与前面两
365
363
个人都不在同一天出生的概率为
,这是因为去掉了两天的缘故。
365
362
再后面的人,生日不与前面任何一个人生日相同的概率依次为
,
365
361
360
365 − 23
342
,
,等等,最后一个人的概率为
,即
。
365
365
365
365
把所有这些分数相乘,就得到所有这些人的生日都不相重合
的概率为
364 363 362
342
×
×
×"×
。
365 365 365
365
用高等数学的方法进行计算,几分钟就可以得出乘积来。如
果不会用高等数学,那只得不辞辛苦地一步步乘出来&①。这费不了
许多时间,结果约为 0.46。这说明生日不相重合的概率稍小于一
半;换句话说,在你这两打朋友中,没有两个人在同一天过生日的
可能性为 46%,而有重合的可能性为 54%。所以,如果你有 25 个
朋友或更多些,但却从来没在同一天被两个人邀请去赴生日晚会,
① 如果会拉计算尺或查对数表,那么请尽可能这样做!
180
第八章 无 序 定 律
那你就可以相当肯定地判断说,要不是他们大多数人不搞什么生
日庆贺,就是他们没有请你前去!
这则生日重合问题提供了一个很好的例子,它说明在判断复
杂事件的概率时,凭想当然来下判断是多么靠不住。我本人曾用
这个问题问过许多人,其中还有不少是卓越的科学家。结果,除一
个人外,其他人都下了从 2 对 1 到 15 对 1 的赌注打赌说,不会发
生这种可能性。如果那位老兄跟他们都打了赌,他可会发起来的!
有一点是要一再强调的:尽管我们能把不同事件的发生概率
按其规则计算出来,并能找出其中最大的概率来,但这并不等于
肯定这个最大者就一定会发生。我们只能推测说“大概”会怎么
样,而不能说“一定”会怎么样,除非把实验重复做上千遍、上
万遍,要是重复几十亿遍就更好。而当只进行有限的几次实验时,
概率定律就不那么管用了。让我们来看一个试图用统计规律来翻
译一小段密码的例子吧。在爱伦坡&*(Edgar Allan Poe)的著名小
说《金甲虫》中,有这么一位勒格让先生。当他在南卡罗来纳州
的荒凉海滩上蹓跶时,发现了一张半埋在--湿--沙里的羊皮纸。这张
羊皮纸在冷时什么也看不出,但在勒格让先生的房间里受了火炉
的烘烤,就显现出一些清晰可辨的红色神秘符号来。符号里有一
个人的头骨,表明这份手稿是一个海盗写的;还有一个山羊头,说
明这个海盗正是有名的基德船长&**。还有几行符号,无疑是指明一
处埋藏珍宝的所在(见图 87)。
我们不妨尊重爱伦坡的威望,姑且承认十七世纪的海盗认识分
号、引号和各种今天常用的符号,如‡、†、¶等等。
勒格让先生很想把这笔钱弄到手,于是便绞尽脑汁想译出这
段密码。最后,他按照英文中各个字母出现的相对频率来进行破
译。他的根据在于:随便找一段英文来,莎士比亚的十四行诗也
* 爱伦坡(1809~1849 年),美国诗人、小说家兼批评家。——译者
** 英文中山羊是 Kid,基德是 Kidd,两者发音和词形都相近,故有此说。——译者
181
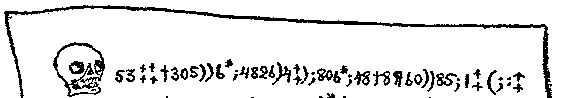

20&世纪科普经典特藏 从一到无穷大
图 87 基德船长的手稿
好,华莱士&*(Edgar Wallace)的侦探小说也好,数一数各字母出
现的次数时,你将发现,字母e出现的次数遥遥领先。其余的字母
按出现次数多少排列如下:
a,o,i,d,h,n,r,s,t,u,y,c,f,g,l,m,w,b,k,
p,q,x,z。
勒格让数了一数基德船长的密码,查出数字 8 出现的次数最
多。“啊哈,”他想,“这就是说,8 大概是 e。”
是的,在这一点上他猜对了。当然,只是大概,而不是一定。
如果这段密码写的是“You will find a lot of gold and coins in an iron
box in woods two thousand yards south from an old hut on Bird island’s north tip”(在鸟岛北端的旧茅屋南面 2 千码处树林中的一个铁箱
内,你可以找到许多金钱)。这里可就连一个 e 也没有!不过概率
论挺帮勒格让先生的忙,他真的猜对了。
第一步走对了,这使勒格让先生信心大增,他就按同样方法
列出了各字母出现的次数表。下面就是按出现频率排列的基德船
长手稿中的符号表&**。
* 华莱士(1875~1932 年),英国小说家兼剧作家。——译者
** 原表中错误较多,现结合图 87 重新统计,制得此表。——译者
182
第八章 无 序 定 律
符号
出现次数
按概率排列顺序
实际字母
8 33 e e
; 26 a t
4 19 o h
‡ 16 i o
) 16 d s
* 12 h n
5 11 n a
6 11 r i
( 10 s r
l 8 t f
† 7 u d
0 6 y l
9 5 c m
2 5 f b
3 4 g g
: 4 l y
? 3 m u
¶
2 w v
– 1 b c
• 1 k p
表中第三栏是按各字母在英语中出现的频率排列的(由高到
低),所以。有理由假设第一栏中的各符号与同一行中的字母逐个
相对应。但是这样一来,基德船长的手稿就成了 ngiiugynddrhaoefr…
这什么意思也没有!
怎么回事呢?是不是基德这个老海盗诡计多端,采用了与英
语字母出现频率不相同的另一套特别的单词呢?根本不是这么回
事。原因很简单,这篇文字太短了,以致统计学的最大概率分布不
起作用。如果基德船长把珍宝以一种很复杂的方法藏起来,然后
用好几页纸写出密码,那么,勒格让先生用概率规则来解这个谜
就会有把握得多。如果这密码写成了一大本书,那就更不成问
题了。
如果扔掷 100 次钱币,你可以很有把握地判断正面朝上的次数
会有 50 次;但如果只扔 4 下,正面就可能出现 3 次或 1 次。实验
次数越多,概率定律就越精确,这时它才成为一条法则。
183
20&世纪科普经典特藏 从一到无穷大
由于这篇密码的字数太少,不足以应用统计法进行分析,勒
格让先生只好凭借英语中单词的细微字母结构来破译。首先他依
然假设出现次数最多的“8”为 e,因为他注意到,“8 8”的组合
在这一小段文字中经常出现(5 次)。大家知道,e 在英语中是经
常双写的,如 meet,fleet,speed,seen,been,agree 等。其次,如
果“8”真的为 e,那它一定会作为“the”的一部分在文中经常出
现。查阅一下手稿,就会发现“; 4 8”这个组合在这段短文中出
现了 7 次,因此我们假设“;”为 t,“4”为 h。
读者们可以自己去破译爱伦坡这篇故事中基德船长的秘密文
字。我把原文和译文写在下面:
“A good glass in the bishop’s hostel
in the devil’s seat。Forty-one degrees and thirteen minutes northeast by north。Main branch seventh limb east side。Shoot from the eye of the
death’s head,A beeline from the tree tbrough the shot fifty feet out”
(主教驿站内魔像座位下有面好镜子。北偏东 41 度 13 分。主干上
朝东的第七根树枝。从骷髅的眼睛开一枪。从那棵树沿子弹方向
走 50 英尺)。
勒格让先生最后译出的字母列在表上最后一栏。可以看出,
它们与概率定律所规定的字母不甚相符,这当然是由于文字篇幅
太短,概率定律没有很多机会发生作用。不过,即使在这个小小的
“统计样品”中,我们也能注意到,各个字母有按概率论的要求排
列的趋势,一旦字母达到很大的数目,这个趋势就会变成确凿的
事实。
关于用大量实验来实际检验概率论的例子大概只有一个,这
就是著名的星条旗与火柴的题目(另外还有一个实例:保险公司
肯定破不了产)。
为了实验这个概率问题,需要有一面美国国旗,即红白条相
间的旗子。如果没有这种旗子,在一大张纸上画上若干道等距的
平行线也可以。再要一盒火柴——什么火柴都成,只要短于平行
线间的距离就可以。此外,还得要一个希腊字母 π。这个字母还有
184
第八章 无 序 定 律
一个意思,它表示圆的周长与直径的比值。你大概知道,这个数等
于 3.1415926535…(还有许多位数字,不过没有必要再继续写
下去)。
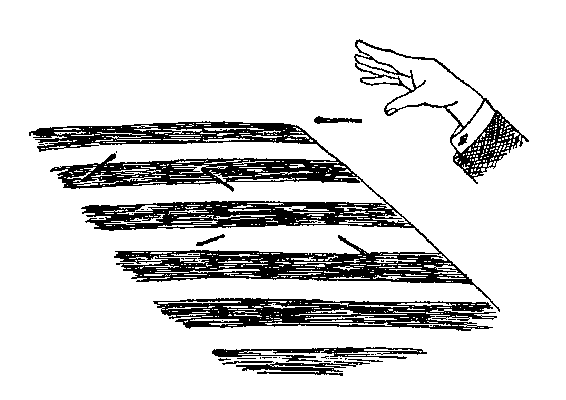
现在把旗子铺在桌子上,扔出一根火柴,让它落在旗子上
(图 88)。它可能完全落在一条带子里,也可能压在两条带子上。
这两种情况发生的机会各为多大呢?
图 88
要想确定概率,首光也得像其他题目那样,弄清各种可能情
况发生的次数各为多少。
但是,火柴落在旗子上,难道不是有无限多种样式吗?怎么能
数得清这各种可能的情况呢?
让我们把这个问题仔细考虑一下。火柴落在条带上的情况,
可由火柴中心点到最近条带边界的距离以及火柴与条带走向所成
的角度来决定,如图 89。图中给出了三种基本类型。为了简便起
见,把火柴长度与条带宽度取相同数值,就说都为 2 英寸吧。如果
火柴中点离边界很近,角度又较大(如例 a),火柴便与边界相交。
如果情况相反,或者角度小(如例 b),或者距离大(如例 c),火
柴就全部落在一条带子里。说精确些,如果火柴的一半长度在竖
直方向的投影大于从火柴中点到最近边界的距离,则火柴与边界
185
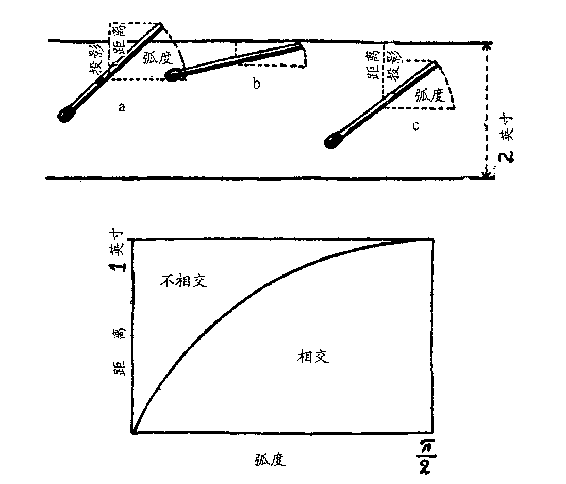
20&世纪科普经典特藏 从一到无穷大
图 89
相交(如 a),反之则不相交(如 b 和 c)。这句话可用图 89 下半
部的图形表示出来。横轴以弧度为单位表示火柴落下的角度,纵
轴是火柴的半长在竖直方向上的投影长度,在三角学中,这个长
度叫做给定角度的正弦。显然,当角度为零时,正弦值也为零,因
π
为这时火柴呈水平方向。当角度为 即直角&①时,火柴取直立位
2
置,与其投影重合,正弦值就是 1。对于处于两者之间的角度,其
π
正弦的值由大家所熟悉的正弦曲线给出。(图 89 只画了从 0 到 这
2
四分之一段曲线。)
有了这条曲线,要计算火柴与边界相交或不相交的两种机会
就很方便了。事实上,我们已经看到(再看图 89 上部的三个例
子),火柴中点离边界的距离如果小于半根火柴的竖直投影,即小
2π
π
① 半径为 1 的圆,周长是直径的 π 倍,即 2π。因此四分之一弧长是
,就是 。
4
2
186
第八章 无 序 定 律
于此时的正弦值,火柴就会与边界相交。这时,代表这个距离和角
度的点在正弦曲线之下。与此相反,火柴完全落在一个条带内时,
相应的点在曲线之上。
按照计算概率的规则,相交机会与不相交机会的比值等于曲
线下的面积与曲线上的面积的比值。也就是说,两个事件的概率,
各等于自己的那一块面积除以整个矩形的面积。可以由数学上证
π
π
明,图中正弦曲线下的面积恰好等于 1。而整个矩形的面积为 ×1 = 。
2
2
所以我们得出结论:火柴(在长度与条带宽度相等时)与边界相交
1
2
的概率为
= 。
π
π
2
π在这个最料想不到的场合跳了出来,这件有趣的事是 18 世
纪的科学家布丰&*(George Louis Leclerc Buffon)最先注意到的,
因此,这个题目也叫做布丰问题。
具体的实验是一位勤谨的意大利数学家拉兹瑞尼(Lazzerini)
进行的。他扔掷了 3407 根火柴,数一数有 2169 根与边界相交。以
×
这个真实数据代入布丰公式,π 就变成了 2 3407 ,即 3.1415929,
2169
与精确值相比,一直到第七位小数才开始不相同!**
这个例子对概率定律的实用性无疑是一个极有趣的明证。但
比起掷几千次钱币,用扔掷总次数除以正面向上的总数可得到 2 这
个结果来,却也有趣不到哪里去。在后一种场合下,你一定会得到
2.000 000…,误差也会和拉兹瑞尼所确定的 π 值的误差一样小。
四、
“ 神 秘 ” 的 熵
从上面这些完全取自日常生活的计算概率的例子里,我们得
* 布丰(1707-1788 年),法国博物学家。——译者
** 原文为 3408 根火柴,经查阅 S. Breuer, G. Zwas&Numerical Mathematics: A Laboratory&Approach&(Cambridge University Press, 1993)p102,拉兹瑞尼于 1901 年宣称共投了 3407
根火柴,相交 2169 根,计算出 π≈3.14154…。——Ken777 注
187
20&世纪科普经典特藏 从一到无穷大
知,当对象的数目很少时,这种推算往往是不怎么灵的;而当数目
增多时,就会越来越准。这就使得在描述由多得数不清的分子或
原子组成的物体时,概率定律就特别有用了,因为即使是我们接
触到的顶小的物质小块,也是由极多的分子或原子组成的。因此,
对于六七个醉鬼,每个人各走上二三十步的情况,统计定律只能
给出大概的结果;而对于每秒钟都经历几十亿次碰撞的几十亿个
染料分子。统计定律却导致了极为严格的扩散定律。我们可以这
样说:试管中那些原先溶解在一半水中的染料,将在扩散过程中
均匀地分布在整个液体中,因为这种均匀分布比原先的分布具有
更大的可能性。
完全出于同样的道理,在你坐着看这本书的房间里,四堵墙
内、天花板下、地板之上的整个空间里均匀地充满着空气。你从来
没有遇到过这些空气突然自行聚拢在某一个角落,使你窒息在椅
子上这种意外情况。不过,这桩令人恐怖的事情并不是绝对不可
能的,它只是极不可能发生而已。
为了弄清这一点,设想有一个房间,被一个想像中的垂直平
面分成两个相等的部分。这时,空气分子在这两个部分中最可能
表现出什么样的分布呢?这个问题当然与前面讨论过的掷钱币问
题一样。任选一个单独分子,它位于房间里左半边或右半边位置
内的机会都是相等的,正如掷一个钱币时,正面或反面朝上的机
会相等一样。
第二个,第三个,以及其他所有分子在不考虑彼此间作用力
的情况下&①,处在房间左半部或右半部的机会都是相等的。这样,
分子在房间两半的分布,正如一大堆钱币的正反分布一样,一半
对一半的分布是最有可能的,我们早已在图 84 中看过这一点了。
我们还看到,扔掷的次数越多(或分子数目越大),50%的可能性
就越来越确定,当数目很大时,可能性就变成了必然性。在一间标
① 由于气体分子间距离很大,空间并不那么挤,所以在一定体积内虽已有一大堆分子,
却并不影响其他分子的进入。
188
第八章 无 序 定 律
准大小的房间里,约有 1027 个分子&①,它们同时聚在右半间(或左
半间)的概率为
27
10
⎛ 1
26
⎞
3
− 1
× 0
≈ 10
⎜ ⎟
,
⎝ 2 ⎠
26
即 1 对 3 10
10 ×
。
另一方面,空气分子以每秒 0.5 公里左右的速度运动,因此,
从房间一端跑到另一端只要 0.01 秒,这也就是说,在一秒钟内,
屋里的分子就会进行一百次重新分布。于是,要得到完全处于右边
(或左边)的分布,需要等上 10299 999 999 999 999 999 999 999 998 秒。要知道宇
宙的年龄迄今为止也只有 1017 秒呀!所以,安安静静地接着读你的
书吧,不必担心发生突然憋死的灾难。
再举一个例子。在桌子上有一杯水。我们知道,由于无规则的
热运动,水分子会以高速向各个可能的方向运动。但是,由于内聚
力的约束,水分子不致逸出。
既然每个分子单独运动的方向完全受概率定律的支配,我们
就应该考虑到这样一种可能性:在某个时刻,杯子上半部的所有
水分子都具有向上的速度,这时下半部的水分子必定都具有向下
的速度&②。此时,在两组水分子的分界面处,内聚力是沿水平方向
的,因此不能阻挡这种“分离的一致愿望”,这时,我们将看到一
个非同寻常的物理现象:上半杯水将以子弹的速度自动飞向天
花板!
另一种可能性是水分子的全部热能偶然地集中在这杯水的上
层,因而上面的水猛烈地沸腾,下面却结了冰。那么,为什么你从
来没有见过这种情景呢?这并不是绝对不可能。而是极不可能发
生。事实上,如果你试试计算一下无规则运动着的分子偶然获得
① 一间 10 英尺宽、15 英尺长、9 英尺高的房间,体积为 1350 立方英尺,或 5×107
厘米 3,可容 5×104 克空气。空气分子的平均重量为 30×1.66×10-14≈5×10-23 克,所以
总分子数为 5×104/5×10-23 = 1027。
② 必须考虑到,由于动量守恒定律排除了所有分子向同一方向运动的可能性,因此水
分子一定是一半对一半的速度分布。
189
20&世纪科普经典特藏 从一到无穷大
相反两组速度的概率,就会得出与全部空气分子聚集在一个角落
的概率相仿的数字;同样,因互相碰撞而使一部分分子失去大部
分动能、同时另外一部分分子得到这部分能量的概率,也是小到
不必理会的。因此我们实际看到的情况的速度分布,正是具有最
大概率的分布。
如果某个物理过程在开始的时候,其分子的位置或速度未处
于最可能的状态,例如,从屋里的一角释放出一些气体,在冷水上
面倒些热水,那么,将会发生一系列物理变化,使整个系统从较不
可能的状态到达最可能的状态。气体将均匀地扩散到整个房间,
上层水的热量将向底层传递,直到全部水取得一致的温度。因此,
我们可以这样说:一切有赖于分子无规则热运动的物理过程都朝
着概率增大的方向发展,而当过程停止,即达到平衡状态时,也就
达到了最大的概率。在屋内空气分布的那个例子中,我们已经看
到,分子各种分布的概率往往是一些很不方便的小数字(如空气
26
聚集在半间屋里的概率为
3 10
10− ×
),因此,我们一般都取它们的
对数。这个数值称为熵,它在所有与物质无规则热运动有关的现
象中起着主导作用。现在,可将前面那些有关物理过程中概率变
化的叙述改写如下:一个物理系统中任何自发的变化,都朝着使
熵增加的方向发展,而最后的平衡状态,则对应于熵的最大可
能值。
这就是著名的嫡定律。也称为热力学第二定律(第一定律是
能量守恒定律)。瞧,这里头并没有什么可怕的东西啊!
从上述所有例子中,我们都可以看出,当熵达到了极大值时,
分子的位置和速度都是完全无规则地分布着,任何使它们的运动
有序化的作法都会引起熵的减小。所以,熵定律又称为无序加剧
定律。熵定律的另一个比较实用的数学公式,可从研究热变为机
械运动的问题中推导出来。大家记得,热就是分子的无规则运动,
因此不难理解,把物体的热能全部转变为宏观运动的机械能,就
等于强迫物体的所有分子都向一个方向运动。我们已经着到,一
190
第八章 无 序 定 律
杯水中有一半自行冲向天花板的可能性是太微乎其微了,实际上
可以看作根本不会发生。因此,虽然机械运动的能量可以完全转
化为热(譬如通过摩擦),热能却永远不会完全变成机械能。这就
排除了所谓“第二类永动机”&①——即在室温下吸收物体热量、降
低物体温度以获得能量来做功——的可能性。因此。不可能设计
出这样一种船,它不用烧煤只靠把海水吸进机舱并吸收它的热
量,就能在锅炉里产生蒸汽,最后再把失掉热量的冰块扔回海里。
那么,真正的蒸汽机是怎样既不违反熵定律、同时又把热变
为功的呢?它之所以能做到这两点,是由于在燃料燃烧所释放的
热中,只有一部分转变成机械能,其余大部分热量或者由废气带
入大气,或者被专门的冷却设备所吸收。这时,整个系统有两种相
反的熵变化:①一部分热转变为活塞-的机械能,这时熵会减小;
②其余热量从锅炉进入冷却设备,这时熵会增大。熵定律说明,系
统的总熵要增大,因此,只要第二个因素比第一个大一些就行了。
我们可以这样来更好地说明这种情况:在 6 英尺高的架子上,放着
一个 5 英磅的重物。按照能量守恒定律,这个重物不可能在没有外
来帮助的情况下,自行升向天花板。然而,它却能向地板上甩下它
自身的一部分,并用这时释放出的能量使其余部分上升。
同样,我们可以使一个系统中某一部分物体的熵减小,只要
这时在剩下的部分中有相应的熵增大来补偿它就行了。换句话说,
对于一些进行无序运动的分子,如果我们不在乎其中一部分变得
更无序的话,那是能够使另外一部分变得有序一些的。的确,在所
有热机械的场合以及在其他许多情况下,我们正是这样做的。
五、统 计 涨 落
通过前一节的讨论,大家想必已经弄清,熵定律及其一切推
论是完全建立在以数量极大的分子为对象的基础上的,只有这样,
① 还有所谓“第一类永动机”,即不用提供能量而能自行做功的机械装置。这是违背
能量守恒定律的。
191
20&世纪科普经典特藏 从一到无穷大
所有基于概率的推测,才会变为几乎绝对肯定的事实。如果物质
的数量很小,这类推测就不那么可信了。
举例来说,如果把前面例子中那个充满空气的大房间,换成边
长各为百分之一微米&①的正方体空间,情况就完全两样了。事实上,
18
−
3
−
×
由于这个立方体的体积为 10-18 立方厘米,只包含 10
10 = 30个
23
3×10−
30
分子。它们全部聚集在一半空间内的概率就变为 ⎛ 1 ⎞
−10
= 10
⎜ ⎟
。
⎝ 2 ⎠
同时,由于这个立方体的体积变小,分子改变混合状态的次
数达到每秒钟 5×1010 次(速度为 0.5 公里每秒,距离只有 10-6 厘
米),因此,这个空间每一秒钟都可能有 10 次空出一半的机会。
至于在这个空间里,分子在某一端比在另一端更集中些的情况就
更可能经常发生了。例如,20 个分子在一头,10 个分子在另一头
(即有一端多出 10 个分子)的情况,就会以
10
⎛ 1 ⎞
10
3
−
10
7
×5×10 = 10 ×5×10 = 5×10
⎜ ⎟
⎝ 2 ⎠
即每秒 5 千万次的频率发生&②。
因此,在小范围内,空气分子的分布远不是均匀的。如果能把
分子放得足够大,我们将会看到,分子不断地在某个地方较为集
中一下子,然后又散开,接着又在其他地方发生某种程度的集中。
这种效应叫做密度涨落,它在许多物理现象中起着重要作用。例
如,当太阳光穿过地球大气时,大气的这种不匀匀性就造成了太
阳光谱中蓝色光的散射,因而使天空带上我们所熟悉的蓝色,同
时使太阳的颜色变得比实际上红一些。这种变红的效应在日落时
尤为显著,因为这时太阳光穿过的大气层最厚。如果不存在密度
涨落,天空就永远是黑的,我们在白天里也能见到星辰。
① 1 微米等于 0.0001 厘米,常用希腊字母 μ 表示。
② 严格地说,这是起码
..有 10 个分子聚在半边的概率。而不是刚好
..有 10 个分子在一端,
另外 20 个在另一端的概率。——译者
192
第八章 无 序 定 律
液体中也同样发生密度涨落和压力涨落,只不过不那么显著
罢了。因此,布朗运动又有了新的解释,即悬浮在水中的微粒之所
以被推来搡去,是由于微粒在各个方面所受到的压力在迅速变化
的缘故。当液体越来越接近沸点时,密度涨落也越来越显著,以致
使液体微呈乳白色。
我们不禁要问,对于这种涨落占主导地位的小物体,熵定律
还起不起作用呢?一个细菌,一生都被分子冲来撞去,它当然会对
我们关于热不能变成机械运动的观点嗤之以鼻的!不过,我们应
该看到,这时熵定律已失去了它本来的意义。而不应认为这个定
律不正确。事实上,这个定律叙述的是:分子运动不能完全转化成
包含有极大量分子的物体的运动。而一个细菌,它比周围分子也
大不了许多,对它来说,热运动和机械运动的区别已经不存在,它
被周围分子冲来撞去,就好像一个人在激动的人群中被大家冲得
东倒西歪一样。如果我们是细菌,那么,只要把我们自己接到一个
飞轮上,就会造成一台第二类永动机。但这时我们已经没有大脑
来想办法利用它了。因此,我们无须因我们不是细菌而感到遗憾
的!
当把熵的增加定律应用到生物体时,仿佛产生了矛盾。事实
上生长着的植物(从空气中)摄入二氧化碳的简单分子,
(从土
壤里)吸收水,并把它们合成复杂的有机物分子以组成自身。从
简单分子到复杂分子意味着熵的减小。在其他一般情况下,如燃
烧木头而把木头分子分解成二氧化碳和水分子时,这个过程是熵
增大的过程。难道植物真的违反了熵的增加定律吗?是不是植物
内部真的像过去的一些哲学家所认为的那样,有种神秘的活力在
帮助它生长呢?
对这个问题所进行的分析表明。并不存在这种矛盾。因为植
物在摄入二氧化碳、水和某些盐类的同时,还吸收了许多阳光。阳
光中除了有能量——它被植物储存在体-内,将来又在植物燃烧时
释放出去——之外,还有所谓“负熵”(低熵),当植物的绿叶将
193
20&世纪科普经典特藏 从一到无穷大
光线吸收进去时,负熵就消失了。因此,在植物叶片中所进行的光
合作用包括以下两个相关的步骤:①太阳的光能转变为复杂有机
物分子的化学能;②太阳光的低熵降低了植物的熵,使简单分子
构筑成复杂分子。用“有序对无序”的术语来说就是:太阳的光
线在被绿叶吸收时,它的内部秩序也被剥夺走,并传给了分子,使
它们能够构成更复杂和更有秩序的分子。植物从无机界得到物质
供应,从阳光得到负熵(秩序);而动物靠吃植物(或其他动物)
来得到负熵,因而可以说是负熵的间接使用者。
194