第十章 不断扩展的视野

一、地球与它的近邻

现在，让我们结束在分子、原子、原子核里的旅行，回到比较

熟悉的不大不小的物体上来。不过，我们还要再旅行一趟，这一次

是向相反的方向，即朝着太阳、星星、遥远的星云和宇宙的深处。

科学在这个方向上的发展，也像在微观世界中的发展一样，使我

们离开所熟悉的物体越来越远，视野也越来越广阔。

在人类文明的初期，所谓的宇宙真是小得可怜。人们认为，大

地是一个大扁盘，四面环绕着海洋，大地就在这洋面上漂浮。大地

的下面是深不可测的海水，上面是天神的住所——天空。这个扁

盘的面积足以把当时的地理知识所知道的地方统统容纳下去。它

包括了地中海和濒海的部分欧洲和非洲，还有亚洲的一小块；大

地的北部以一脉高山为界，太阳在夜间就在山后的“世界洋”海

面上休憩。图 104 相当准确地表示出古代人关于世界面貌的概念。

但是，公元 3 世纪，有一个人对这种简单而被人们普遍接受的世界

观提出了异议。他就是著名的希腊哲人（当时这个名称是用来称呼

科学家的）亚里士多德（Aristotle）。

亚里士多德在他的著作《天论》里，表述了这样一个理论：

大地实际上是一个球体，一部分是陆地，一部分为水域，外面被空

气包围着。他引证了许多现象来证明自己的观点，这些现象在今

天的人们看来是很熟悉的，似乎还显得有些琐碎。他指出，一艘船

当消失在地平线上时，总是在船身已看不见时，桅杆还露在水面

上。这说明洋面不是平的，而是弯曲的。他还指出，月食一定是地

226

第十章 不断扩展的视野

图 104 古代人认为世界只有这么大

球的阴影掠过这个卫星的表面时引起的。既然这个阴影是圆的，

大地本身也应该是圆的。但是，当时并没有几个人相信他的话。人

们不能理解，如果他的说法确实不错，那么，住在球体另一端

（即所谓对蹠点，对我们来说是澳大利亚&*）的人怎么会头朝下走

路呢？难道他们掉不下去吗？为什么那里的水不会流向天空呢

（图 105）？

你瞧，当时的人们并没有理解到，东西的下落是由于受到了

地球的吸引力。对于他们来说，“上”和“下”是空间的绝对方

向，不论在哪里都是一样的。在他们看来，说把我们这个世界走上

一半远，“上”就会变成“下”，“下”就会变成“上”，这简直是

在说胡话。当时，人们对亚里士多德这种观点的看法，正像今天某

些人对爱因斯坦相对论的看法一样。当时，重物下坠的现象，被解

释成一切物体都有向下运动的“自然倾向”，而不是像现在这样解

释成受到地球的吸引。因此，当你竟然敢冒险跑到这个地球的下

面一半去时，就会向下掉到蓝天中去！对老观念进行调整的工作

* 这是对美国而言，中国的对蹠点是巴西。——译者

227

20&世纪科普经典特藏 从一到无穷大

图 105 反对大地为球形的论点

是异常艰难的，新观念遭到了极为强烈的反对，甚至到了 15 世纪，

即亚里士多德死后两千年，还有人用地球对面的人头朝下站着的

画片，来嘲笑大地是球形的理论。就连伟大的哥伦布&*（Christo-

pher Columbus）在动身前去寻找通往印度的“另一条路”时，也

未必意识到他自己的计划是健全的，而且他的行程也因美洲大陆

的阻挡而未能全部实现。直到麦哲伦&**（Ferdinand de Magellan）进

* 哥伦布（1451～1506 年），意大利航海家，于 1492 年发现“新大陆”美洲。——译者

** 麦哲伦（1480～1521 年），葡萄牙航海家，于 1519 年首次率船队完成环球航行，麦

哲伦本人于 1521 年死于旅途，但船员继续航行，于次年返回欧洲。——译者

228

第十章 不断扩展的视野

行了著名的环球航行后，人们对大地是球体的怀疑才最后消失掉。

当人们首次意识到大地是球体后，自然要给自己提出这样的

问题：这个球体底有多大？和当时已知世界相比情况如何？但是，

古希腊的哲人们显然是无法进行环球旅行的，那又怎么来量度地

球的尺寸呢？

嘿！有一个办法。这个办法是公元前 3 世纪希腊著名科学家

埃拉托色尼最先发现的。他住在希腊当时的殖民地，埃及的亚历

山大里亚城。当时有个塞-恩城，位于亚历山大里亚城以南五千斯

塔迪姆远的尼罗河上游&*。他听那里的居民讲，在夏至那一天正

午，太阳正好悬在头顶，凡是直立的物体都没有影子。另外，埃

拉托色尼又知道，这种事情从来没有在亚历山大里亚发生过；就

是在夏至那一天，太阳离天顶（即头顶正上方）也有 7°的角距

离，这是整个圆周的 1/50 左右。埃拉托色尼从大地是圆形的假设

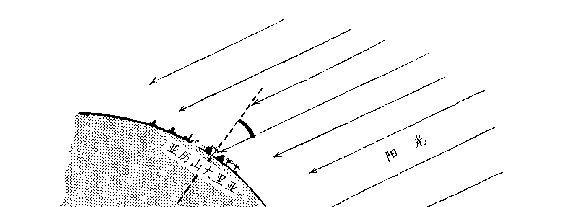
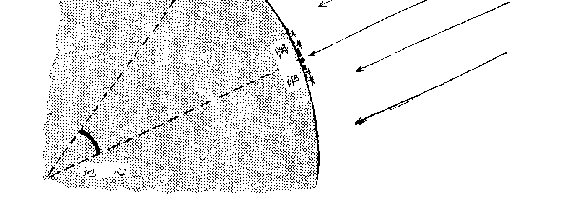
出发，给这个事实作了一个很简单的解释，这很容易从图 106 上

看懂。事实上，既然两座城市之间的地面是弯曲的，竖直射向塞-

恩的阳光一定会和位于北方的亚历山大里亚成一定的交角。从地

球中心画两条直线，一条引向塞-恩，一条引向亚历山大里亚，则

从图上还可以看出，两条引线的夹角等于通过亚历山大里亚的那

条引线（即此处的天顶方向）和太阳正射塞-恩时的光线之间的

夹角。

由于这个角是整个圆周的 1/50，整个圆周就应该是两城间距

离的 50 倍，即 250 000 斯塔迪姆。一斯塔迪姆约为 1/10 英里，所

以，埃拉托色尼所得到的结果相当于 25 000 英里，即 40 000 公里，

和现代的数值真是非常相近。

然而，对地球进行第一次测量所得到的结果，重要的倒不在

于它是如何精确，而是它使人们发现地球真是太大了。瞧，它的

总面积一定比当时已知的全部陆地面积大几百倍呢。这能是真的

* 即现今阿斯旺水坝附近。——译者

229

20&世纪科普经典特藏 从一到无穷大

图 106

吗？如果是真的，那么，在已知的世界之外又是些什么呢？

说到天文学距离，找们先得熟悉一下什么叫视差位移（简称

视差）。这个名称听起来有点吓人，但实际上，视差是件简单而

有用的东西。

我们可以从穿针引线的尝试来认识视差。试试闭上一只眼来

穿针，你很快就会发现这么干并不怎么有把握：你手中的线头不

是跑到针眼后头老远，就是在还不到针眼时就想把线穿进去。只

凭一只眼睛是判断不出针和线离我们有多远的。但是，如果睁开

双眼，这件事就很容易做到，至少是很容易学会怎样作到的。当

用两只眼睛观察一个物体时，人们会自动地把两只眼睛的视线都

聚焦在这个物体上；物体越近，两只眼珠就转动得更接近一些。

而进行这种调整时眼球上肌肉所产生的感觉，就会相当可靠地告

诉你这段距离是多少。

如果你不同时用两只眼睛来看，而是分别用左、右眼来看，

你就会看到物体（在此例中为针）相对于后面背景（如房间里的

230

第十章 不断扩展的视野

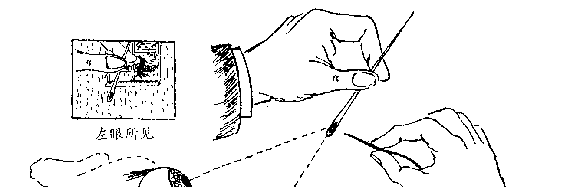
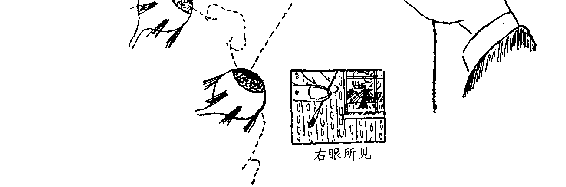
窗子）的位置是不一样的。这个效应就叫做视差位移，大家一定

都很熟悉。如果你从来没听说过，不妨自己试验一下，或看一看

图 107 所示的左眼和右眼分别看到的针和窗。物体越远，视差位

移越小。因此，我们可以用这种效应来测量距离。视差位移是可

以用弧度表示出来的，这要比靠眼球肌肉的感觉来判断距离的简

单方式准确得多。不过，我们的两只眼睛仅相距 3 英寸左右，因此，

当物体的距离在几英尺开外时就不能量得很准了。这是因为物体

越远，两只眼睛的视线就越趋于平行，视差位移也就越不显著。

为了测量更远的距离，就应该该把眼睛分得开一些，以增大视差位

移的角度。不，这可用不着做外科手术，只要用几面镜子就行了。

图 107

在图 108 上，我们能看到海军使用的这样一种测量敌舰距离

的装置（在雷达发明以前）。这是一根长筒，两眼前面的位置上

各有一面镜子（A，A′），两端各有一面镜子（B，B′）。从这样

一架测距仪上，真能够作到一只眼在 B 处看，另一眼在 B′处看

了。这样，你双眼间的距离——所谓光学基线——就显著增大了，

因此，所能估算的距离也就会长得多。当然，水兵们是不会单靠

231

20&世纪科普经典特藏 从一到无穷大

眼球肌肉的感觉来下判断的。测距仪上装有特殊部件和刻度盘，

这样能极精确地测定视差。

图 108

这种海军测距仪，即使对于出现在地平线上的敌舰，也是

很有把握测准的。然而，用它来测量那怕是最近的天体——月

亮——效果也不那么好。事实上，要想观测月亮在恒星背景上出

现的视差，光学基线（也就是两眼间的距离）非得有几百英里不

行。当然，我们没有必要搞出一套光学系统，使得我们能用一只

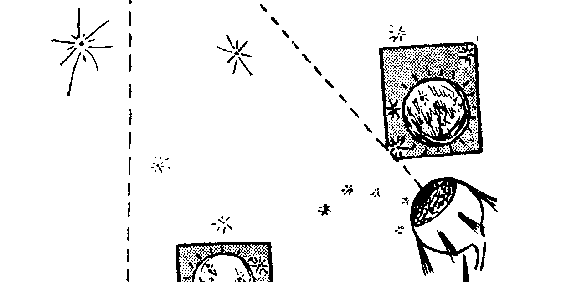
眼在华盛顿看，另一只眼在纽约看。只要在两地同时拍摄一张位

于群星中的月亮照片就行了。把这两张照片放到立体镜&*里，就

能看到月亮悬浮在群星前面。天文学家们就从这样两张在地球上

两个地点同时拍摄的月亮和星星的照片（图 109），算出从地球一

条直径的两端来看月亮的视差是 1°24′5″，由此得知地球和月亮的

距离为地球直径的 30.14 倍，即 384 403 公里，或 238 857 英里。

根据这个距离和观测到的角直径，我们算出这颗地球卫星的

直径为地球直径的四分之一。它的表面积为地球面积的十六分之

一，这约等于非洲大陆的面积。

* 立体镜是一种观看图片立体效果的装置。把两张从两个适当角度拍来的同一物体的

照片放到里边，两眼分别观看其中一张，就能产生立体效果。——译者

232

第十章 不断扩展的视野

图 109

用同样的方法也能求出太阳离我们的距离。当然，由于太阳

要远得多，测量就更加困难一些。天文学家们测出这个距离是

149 450 000 公里（92 870 000 英里），也就是月地距离的 385 倍。

正是由于距离这么大，太阳看起来才和月亮差不多大小，实际上，

太阳要大得多，它的直径是地球直径的 109 倍。

233

20&世纪科普经典特藏 从一到无穷大

如果太阳是个大南瓜，地球就是颗豌豆，月亮则是粒罂粟籽，

而纽约的帝国大厦只不过是在显微镜下才能看到的顶小的细菌。

不妨顺便提一下，古希腊有个进步哲人阿那萨古腊（Anaxago-

ras），仅仅因为在讲学时提出太阳是个像希腊那样大小的火球，

就遭到了流放的惩罚，并且还受到处死的威胁呢！

天文学家们还用同样的方法计算出了太阳系中各行星与太阳

的距离。1930 年发现的最远的行星冥王星，离太阳的距离约为地

球和太阳的距离的 40 倍，准确点说，这个距离是 3 668 000 000 英

里。

二、银 河 系

再向空间迈出一步，就从行星走到恒星世界了。视差方法在

这里仍然可以应用，不过，即使是离我们最近的恒星，同我们的

距离也是很远很远的，因此，即便是在地球上距离最远的两点

（地球的两侧）进行观测，也无法在广袤的星际背景上找出什么

明显的视差。然而，我们还是有办法的。如果我们根据地球的

尺寸求出它绕日轨道的大小，那么，为什么不用这个轨道去求恒

星的距离呢？换句话说，从地球轨道的两端去观测恒星，是否可

以发现一、两颗恒星的相对位移呢？当然，要这样做，两次观测的

时间要相隔半年之久，但那又有什么不可以的呢？

怀着这样的想法，德国天文学家贝塞-尔（Friedrich Wilhelm

Bessel）在 1938 年开始对相隔半年的星空进行了比较。开始他并

不走运，他所选定的目标都未显示出任何明显的视差。这说明它

们都太远了，即使以地球轨道直径为光学基线也无济于事。可是，

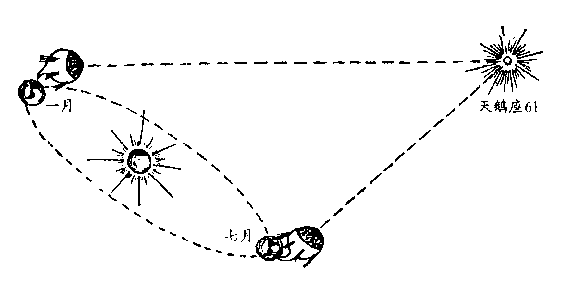
瞧，这里有一颗恒星，它在天文学花名册上叫做天鹅座 61（也就

是天鹅座的第 61 颗暗星），它的位置和半年前稍有不同（图 110）。

再过半年进行观测时，这颗星又回到了老地方。可见，这一

定是视差效应无疑。因此，贝塞-尔就成了拿着尺子跨出太阳系进

入星际空间的第一个人。

234

第十章 不断扩展的视野

图 110

在半年间观察到的天鹅座 61 的位移是很小的，只有 0.6 弧

秒&①，这就是你在看 500 英里之外的一个人时视线所张的角度（如

果你能看见这个人的话）！不过，天文仪器是很精密的，就连这样

小的角度也能以极高的精确度测出来。根据测出的视差和地球轨

道直径的已知数值，贝塞-尔推算出这颗星在 103 000 000 000 000

公里之外，比太阳还远 690 000 倍！这个数字的意义可不容易体

会。在我们打过的那个比方中，太阳是个南瓜，在离它 200 英尺

远的地方有颗豌豆大小的地球在转动，而这颗恒星则处在 3 万英

里远的地方！

在天文学上，往往把很大的距离表示成光线走过这段距离所

用的时间（光的速度为 300 000 公里每秒）。光线绕地球一周只用

1/7 秒，从月亮到地球只要 1 秒出头，从太阳到地球也不过是 8

分钟左右。而从我们在宇宙中的近邻天鹅座 61 来的光，差不多要

11 年才能到达我们这里。如果天鹅座 61 在一场宇宙灾难中熄灭

了，或者在一团烈焰中爆炸了（这在恒星中是常常发生的），那

么，我们只有经过漫长的 11 年之后，才能从高速穿过星际空间到

达地球的爆炸闪光和最后一线光芒得知，有一颗恒星已不复存在

了。

① 精确值为 0.600″±0.06″。

235

20&世纪科普经典特藏 从一到无穷大

贝塞-尔根据测得的天鹅座 61 的距离，计算出这颗在黑暗的夜

室中静悄悄地闪烁着的微弱光点，原来竟是光度仅比太阳小一

点、大小只差 30％的星体。这对于哥白尼（Copernicus）关于太

阳仅仅是散布在无垠空间中、彼此遥遥相距的无数星体中的一个

星体这样一个革命性论点，是第一个直接的证据。

继贝塞-尔的发现之后，又有许多恒星的视差被测出来了。有

几颗比天鹅座 61 近一些，最近的是半人马座&α（半人马座内最明

亮的星，即南门二），它离我们只有 4.3 光年。它在大小和光度

上都与太阳相近。其他恒星大都要远得多，远到即使用地球轨道

的直径作为光学基线，也测不出视差来。

恒星在大小和光度上的差别也很悬殊。大的有比太阳大 400

倍、亮 3600 倍的猎户座&α（即参宿四，300 光年）之类光辉夺目

的巨星，小的有比地球还小，并比太阳暗 10 000 倍的范玛伦星

（直径只有地球的 75％，距我们 13 光年）之类昏暗的矮星。

现在我们来谈一谈恒星的数目这一个重要的问题。许多人，

可能包括读者诸君在内，都以为天上星星数不清。然而，正如其

他许多流行的看法一样，这种看法也是大错而特错的，起码就肉

眼可见的星星而论是如此。事实上，从南北两个半球可直接看到

的星星加起来只有六七千颗左右；又因为在任何一处地面上只能

看到一半天空，还因为地平线附近大气吸收光线的结果使能见度

降低，所以，就是在晴朗的无月之夜，凭肉眼也只能看到 2 千颗

左右的星星。因此，以每秒钟一颗的速度勤快地数下去，半小时

左右就可把它们数完了。

不过，如果用普通的双筒望远镜来观测，就可以多看到 5 万

颗星，而一架口径为两英寸半的望远镜，则会显示出 100 多万颗

来。从安放在加利福尼亚州威尔逊山天文台的那架有名的 100 英

寸口径的望远镜里观测时，能看到的星星就会达到 5 亿颗。一秒

钟数一颗，每天从日落数到天明，一个天文学家要数上一个世纪

才能把它们数完！

236

第十章 不断扩展的视野

当然，不会有人真的通过望远镜去一颗颗地数数，星星的总

数是把几个不同区域内星星实际数目的平均值推广到整个星空而

得出的。

一百多年前，著名的英国天文学家赫歇耳（William Herschel）

用自制的大型望远镜观察星空的时候，注意到了这样一个事实：

大部分肉眼可见的星星都分布在横跨天际的一条叫做银河的微弱

光带内。由于他的研究，天文学上才确立了这样的概念：这条银

河并不是天空中的一道普通星云&*，而是由为数极多、距离很远、

因而暗到肉眼不能一一分辨的恒星组成的。

使用强大的望远镜，我们能看到银河是由为数很多的一颗颗

恒星组成的；望远镜越强大，看到的星星就越多。但是，银河的

主要部分依然处在一片模糊之中。然而，如果就此以为，在银河

范围内的星星比其他地方的星星稠密些，那可是大错而特错了。

实际上，星星在某个区域内看起来数目比较多的现象，并不真的

是分布比较集中，而是星星在这个方向上分布得深远些。在沿银

河伸展的方向上，星星一直伸展到目力（在望远镜的帮助下）所

及的边缘，而在其他方向，星星并不伸展到视力的界限；在它

们的后边，几乎是空虚无物的空间。

沿银河伸展的方向看去，就好像在密林里向远处张望，看到

的是许多重叠交织的树枝树干，形成一片连续的背景；而沿其他

方向，则能看到一块块空间，正如我们在树林里面，透过头上的

枝叶，可以看见一块块的蓝天一样。

可见，这一大群星体在空间里占据了一个扁平的区域；在银

河平面内伸向很远的地方，而在垂直于这个平面的方向上，相对

说来范围并不那么远。太阳只不过是银河中无足轻重的一员。

经过几代天文学家们的仔细研究，已得到了结论说，银河包含

有大约 40 000 000 000 颗恒星，它们分布在一个凸透镜形的区域

* 星云一般是稀薄的气体和尘埃在宇宙空间中形成的不规则巨团。——译者

237

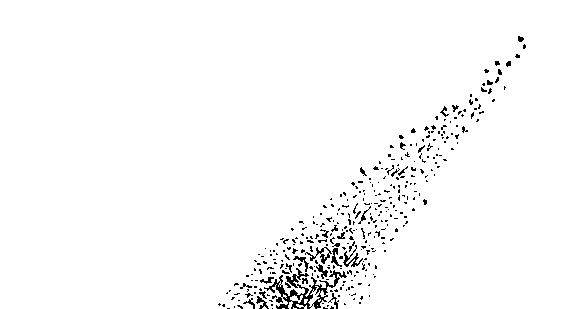
20&世纪科普经典特藏 从一到无穷大

内，直径有 100 000 光年左右，厚度在 5000～10 000 光年上下。

我们还得知，太阳根本不处在这个大星系的中心，而是位于靠近

外缘的部分。对我们人类的自尊心来说，这可真是当头一棒啊！

我们想用图 111 来告诉读者们，银河这个由恒星组成的大蜂

窝看起来是什么样子。顺便提一下，银河在科学的语言中应该用

银河系这个名称来代替。图中的银河系是缩小了 1 万亿亿倍的。

而且，代表恒星的点也比 4 百亿少得多，这当然是出自印刷角度

的考虑。

图 111 一位天文学家在观察银河系。银河系被缩小了

100 000 000 000 000 000 000 倍。太阳的位置大致就在天文学家的头部

这个由一大群星星所组成的银河系，它的最显著的一个性质，

就是它也和我们这个太阳系一样，处于迅速的旋转状态中。就像

238

第十章 不断扩展的视野

水星、地球、木星和其他行星沿着近于圆形的轨道绕太阳运行一

样，组成银河的几百亿颗星也绕着所谓银心转动。这个旋转中心

位于人马座的方向上。因为在你顺着天河跨过天空的方向找去

时，会发现它那雾濛濛的模糊外形在接近人马座时变得越来越

宽，这表明你现在望见的正是这个凸透镜状物体的中心部分（图

111 中的那位天文学家正是朝这个方向看去的）。

银心看起来是个什么样子呢？我们现在还不知道，因为这一

部分不幸被浓云一般暗黑的星际悬浮物质所遮盖了。事实上，如

果观察人马座区域中银河变厚的那一部分&①，你起初会认为这条

神话中的河分成两支“单航道”。但这种分汊并不是真实情况，

这种印象是由悬浮在我们和银心之间的星际尘埃和气体的暗云块

造成的。它不同于银河两侧的黑暗区，那些暗区是空间的暗黑背

景，而这里却是不透明的黑云。在中间那片黑云上可看到的几颗

星星，其实是位于我们和黑云之间的（图 112）。

图 112 向银心看去，给人的感觉是这条神话中的河分成两汊

看不到这个神秘的、连太阳都绕着它旋转的银心以及其他数

十亿个恒星，当然是件太憾事。不过，通过对散布在银河之外的

其他星系的观察，我们也能够大致判断出我们这个银心的样子。

在银心中，并没有一个像我们这个行星系中的太阳一样的超级巨

星在控制着星系的所有成员。对其他星系的研究（以后我们要讲

① 这种观察在初夏的晴夜进行最为有利。

239

20&世纪科普经典特藏 从一到无穷大

到）表明，它们的中心也是由许多恒星组成的，不过这里的恒星

要比太阳附近的边缘地区拥挤得多就是了。如果把行星系统比做

由太阳统治着的封建帝国，那么，银河系就像是一个民主国家，

有一些星星占据了有影响的中心位置，其他星星则只好屈尊于外

围的卑下社会地位。

如上所述，所有的恒星，包括我们的太阳，统统在巨大的轨

道上围绕银心而运转。可是，这是怎么证明出来的呢？这些星星

的轨道半径有多大呢？绕上一周需要多长时间呢？

所有这些问题，都由荷兰天文学家欧尔特（Jan Hendrik Oort）

在几十年前作出了回答。他使用的观察方法与哥白尼用以考察太

阳系的方法很相似。

先看一看哥白尼的思考方式。古代巴比伦人和埃及人，以及

其他古代民族，都注意到木星、土星一类大行星在天空运行的奇

特路线。它们似乎先是顺着太阳行进的方向沿着椭圆形轨道前

进，然后突然停下来，向后走一段，再折回来朝原来的方向行进。

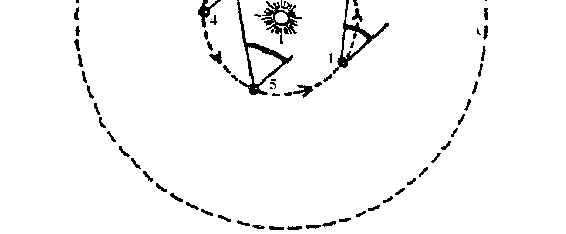
在图 113 下部，我们画出了土星在两年时间内的大致路线（土星

运转周期为 29.5 年）。过去，出于宗教偏见把地球当作宇宙的中

心，认为所有行星和太阳都绕着地球旋转，对于上面这种奇怪的

运动，只好用行星轨道是一圈一圈的环套连成的假设来进行解

释。

但是，哥白尼的目光却敏锐得多。他以天才的思想解释道：

这种神秘的连环现象，是由于地球和其他各行星都围绕太阳作简

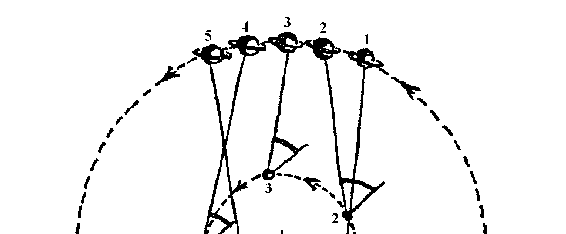
单圆周运动的结果。看看图 113 的上部，这种解释就好理解了。

图的中心是太阳，地球（小一些的那个球）在小圆上运动，

土星（有环者）以相同的方向在大圆上运转。数字 l，2，3，4，

5 标出了地球和土星在一年中的几个位置。我们要记住，土星的

运行比地球慢许多。从地球各个位置上引出的那些垂直线是指向

某一颗固定恒星的。从地球的各个位置向相应时刻的土星上引连

线，我们看出这两个方向（指向土星和固定恒星）间的夹角先是

240

第十章 不断扩展的视野

图 113

增大，继而减小，然后又增大。因此，那种环套式行进的表面现

象并不意味着土星运动有任何特别之处，只不过是我们在本身也

在运动着的地球上观测土星时的角度不尽相同罢了。

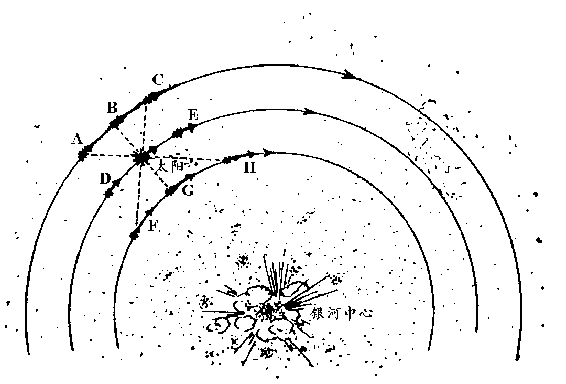
欧尔特关于银河系中恒星作圆周运动的论点，可从图 114 弄

明白。在图的下方，可以看到银心（有暗云之类的东西），环绕

中心，整个图上都有恒星。三个圆弧代表着距中心不同距离的恒

星轨道，中间的那个圆表示太阳的路线。

我们来看八颗恒星（以四射的光芒标出，以别于其他恒星），

其中的两颗与太阳在同一轨道上运动，一颗超前一些，一颗落后

一些；其他的恒星，或者轨道远一些，或者近一些，如图 114 所

示。要记住，由于万有引力的作用，外围恒星的速度比太阳小，

内层恒星的速度比太阳大（图上用箭头的长短表示）。

这八颗恒星的运动情况，从太阳也就是从地球上看来，是怎

样的呢？我们这里所指的是恒星沿观察者视线方向的运动，这可

241

20&世纪科普经典特藏 从一到无穷大

图 114

以根据多普勒效应&①很容易地看明白。第一点，与太阳同轨道同速

度的两颗恒星（标以D和E的两颗）显然相对于太阳（或地球）

是静止的。这一点也适用于与太阳处于同一半径上的两颗（B和

G），因为它们与太阳的运动方向平行，在观测方向没有速度分

量。处于外围的恒星A和C又如何呢？因为它们都以低于太阳运

动的速度运行，从图上可以清楚地看出，A 会逐渐落后，C 会被

太阳赶上。因此，到 A 的距离会增大，到 C 的距离会减小，而从

这两颗恒星射来的光线则会分别显示多普勒红移效应和紫移效

应。对于内层的恒星 F 和 H，情况正好相反，F 会表现出紫移效

应，H 会表现出红移效应。

假定刚才所描述的现象是仅仅由于恒星的圆周运动所引起的，

那么，如果恒星确实有这种运动，我们就不仅能证明这种假设，

还能计算出恒星运动的轨道和速度来。通过搜集天空中各颗恒星

的视运动的资料，欧尔特证明了它所假设的红移和紫移这两种多

普勒效应确实存在，从而确凿地证明了银河系的旋转。

① 见第 314 有关介绍多普勒效应的部分。

242

第十章 不断扩展的视野

同样也能够证明，银河系的旋转也会影响到各恒星沿垂直于

视线方向的视速度。尽管精确测定这个速度分量要困难得多（因

为远处的恒星哪怕具有很大的线速度，也只能产生极小的角位

移），这种现象也被欧尔特和其他人观察到了。

精确地测定出恒星运动的欧尔特效应，我们就能够求出恒星

轨道的大小及运行周期。现在已经知道，太阳以人马座为中心的

运行半径是 30 000 光年，这相当于整个银河系半径的三分之二。

太阳绕银心运行一周的时间为两亿年左右。这当然是段很长的时

间，不过要知道，我们这个银河系已有 50 亿岁了；在这段期间

内，我们的太阳已带着它的行星家族一起转了 20 多圈。如果照地

球年这个术语的定义，把太阳公转一周的时间称为“太阳年”，

我们就可以说，我们这个宇宙只有 20 多岁。在恒星的世界上，事

情的确是发生得很缓慢的，因此，用太阳年作为记载宇宙历史的

时间单位，倒是颇为方便的。

三、走向未知的边界

前面已经提到过，我们这个银河系并不是唯一的在巨大的宇

宙空间飘浮的、孤立的恒星社会。望远镜的研究已经在空间深

处揭示出了许多巨大的系统，它们和我们这个太阳所属的星群很

相似。距我们最近的一个是著名的仙女座星云，它可直接用肉眼

看到。它的样子是一个又小又暗的相当长的模糊形体。图版Ⅶ的

a 和 b 是用威尔逊山天文台的大望远镜所拍摄到的两个这样的天

体，它们是后发座星云的侧观和大熊星座星云的正观。可以注意

到，它们有典型的旋涡结构，而在总体上构成了和我们这个银河

系一样的凸透镜形，因此这些星云被称为“旋涡状星云”。有许

多证据表明，我们的这个银河系也是这样一个旋涡体。当然，要

从内部来确定这一点是件很困难的工作，但我们还是了解到，太

阳非常可能位于我们这个“银河大星云”的一条旋涡臂的末端

上。

243

20&世纪科普经典特藏 从一到无穷大

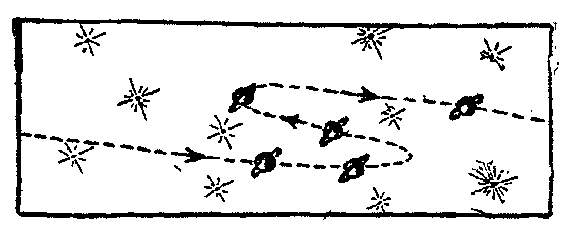
在很长一段时间内，天文学家们并未意识到这类旋涡星云是

与我们这个银河系相类似的巨大星系，却把它们和一般的弥散星

云混为一谈，后者是散布在空间中的微尘所形成的巨大云状物，

如悬浮在银河内恒星之间的猎户座星云。但是，人们后来发现，

这些看起雾濛濛的旋涡状天体根本不是尘埃和雾气。使用最高倍

的望远镜，可以看到一个个小点，这证明它们是由单独的恒星组

成的。只过它们离我们太远了，无法用视差法求出距离来。

看来，我们量度天体距离的手段好像是到此为止了。但是，

不！在科学研究中，当我们在某个无法克服的困难前面停止下来

时，耽搁往往只是暂时的；人们总是有新的发现，从而使我们再

前进下去。在这里，哈佛大学的天文学家沙普勒（Harlow Shap-

ley）又找到了一根新式的“量天尺”——所谓脉动星或造父变

星&①。

天上星，难数清。大多数星星宁静地吐着光辉，但有一些星

星，它们的光度则有规律地发生明暗的变化。这些巨大的星体像

心脏一样规则地搏动着，它的亮度也随着搏动而进行周期性变

化&②。恒星越大，脉动周期越长；这就像钟摆越长，摆动就越慢

一样。很小的恒星（就恒星而论）几小时就完成一个周期，巨星

则需要很多年。而且，既然恒星越大就越明亮，因此，造父变星

的脉动周期与平均亮度之间一定存在着相互关系。通过观测离我

们相当近、因而能够直接测出距离和绝对亮度的仙王座造父变

星，这种关系是可以确定下来的。

如果我们发观了一颗脉动星，它的距离超出了视差法的量程，

那么，我们只要从望远镜里观测它的脉动周期，就能知道它的真

实亮度，再把它与视亮度对比，就可以立即知道它的距离。沙普

勒就是用这种机敏的方法，成功地测出了银河内的极远距离，并

有效地估计出我们这整个星系的大小。

① 这种星的脉动变化现象是首先在仙王座的&β&星（造父一）上发现的，因而就以此命名。

② 不要和交食变星、即两个互相围绕对方转动的恒星的周期性掩食现象相混。

244

第十章 不断扩展的视野

当沙普勒用这种方法来测量仙女座星云中的几颗脉动星时，

所得到的结果使他大吃一惊：从地球到这几颗恒星的距离——这

当然也就是到仙女座星云本身的距离——竟达 1 700 000 光年。这

就是说，它比银河系的直径还要大得多。仙女座星云的体积原来

只比我们这个银河系略小一些。本书图版Ⅶ上的两个旋涡状星云

还要更远，它们的直径也和仙女座星云不相上下。

这个发现宣判了原先那种认为旋涡状星云是银河系内的“小

傢伙”的观点的死刑，并确立了它们作为类似于银河系的独立星

系的地位。如果在仙女座星云中数以亿计的恒星当中，有一颗恒

星所属的行星上有“人类”存在，那么，他们所看到的我们这个

银河系的形状，就和我们现在看他那个星系的形状差不多一样。

对此，天文学家现在已不再有什么怀疑了。

由于天文学家们，特别是著名的星系观测家、威尔逊天文台

的 E. 哈勃（Edwin Powell Hubble）的探索，这些遥远的恒星社团

已向我们披露了许多有趣而重要的事实。第一点，由强大的望远

镜所观测到的为数众多——比用肉眼能看到的星星还多——的星

系并不都是旋涡状的，而且种类还不少。有球状星系，它看起来

像个边界模糊的圆盘；有扁平程度各不相同的椭球状星系；即使

是旋涡状的，其“绕卷的松紧程度”也有所不同。此外，还有形

状奇特的“棒旋星系”。

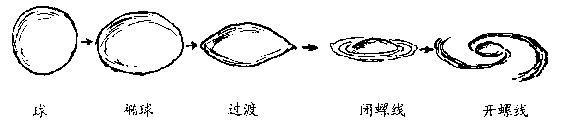
把观测到的这各种星系类型排列起来，得到一个极为重要的

事实（图 115）：这个序列可能表示了这些巨大星系的各个不同的

演化阶段。

图 115 银河系在正常进化中各个阶段

245

20&世纪科普经典特藏 从一到无穷大

关于星系演化的详细过程，我们还远远没有达到了解的地步，

不过，演化很可能是由于不断收缩而造成的。大家都知道，当一

团缓慢旋转的球状气体逐步收缩时，它的旋转速度会加快，形状

也随之变为椭球体。当收缩到一定阶段，即当椭球的极轴半径与

赤道半径的比值达到 7／10 时，就会在赤道上出现一道明显的棱，

成为凸透镜状的物体。再进一步收缩，旋转的气体物质就会沿棱

圈方向散开，在赤道面上形成一道薄薄的气体帘幕，同时整团气

体仍大体保持着透镜形状不变。

英国著名物理学家兼天文学家金斯（James Hopwood Jeans）

从数学上证明了上面这些说法对于旋转的球状气体是成立的。同

时，这种论述也可以原封不动地应用到星系这类巨大的星云上

去。事实上，让单个恒星扮演分子的角色，我们就可以把这样密

集在一起的亿万颗恒星看成一团气体了。

把金斯的理论计算和沙普勒对星系的实际分类对照一下，就

会发现两者完全吻合。具体地说，我们已发现，所观测到的最扁

平的椭球状星云，其半径之比为 7/10（E7）；而且这时开始在赤

道位置上出现明显的棱圈。至于演化后期出现的旋臂，显然是由

迅速旋转时被甩出的物质形成的。不过，迄今为止，我们还不能

非常圆满地解释为什么会出现这种臂，它们是怎样形成的，以及

造成普通旋臂和棒型旋臂的差别的原因。

对这些星系的构造、运动和各部分组成的了解，还需要做许

多研究工作。例如，有这么一个有趣的现象：前几年，威尔逊山

天文台的天文学家巴德（Walter Baade）指出，旋涡状星云的中心

部分（核）的恒星和球状，椭球状星系的恒星属于同一种类型，

但是在旋臂内部出现了新的成员。这种“旋臂型”成员因其又热

又亮而和中心部分的成员不同，是所谓“蓝巨星”。在旋涡星系

的中心部分和球状、椭球状星系的内部找不到这种恒星。以后

（在第十一章）我们将看到，蓝巨星极可能表示新诞生不久的恒

星，因此，我们有理由认为，旋臂是星空新成员的产房。可以假

246

第十章 不断扩展的视野

设，从正在收缩的椭球状星系那膨胀的“腰部”甩出来的物质，

有一大部分是气体，它们来到寒冷的星际空间后，就凝缩为一块

块巨大的天体。这些天体以后又经收缩，变得炽热而明亮。

在第十一章中，我们还要再回过头来探讨恒星的产生和经历。

现在，我们应该考虑一下星系在广大宇宙空间内的大致分布。

先得说明一点：通过观测脉动星来测量距离的方法，在用来

判断银河附近的一些星系时得到了极好的结果。然而，当进入空

间的更深处时，这种方法就变得很不灵了，因为这时的距离已大

到即使用最强大的望远镜也不能分辨出单个星星的程度。这时所

看到的整个星系只不过是一团小小的长条星云。在这种情况下，

我们只能凭所见到的星系的大小来判断距离，因为星系并不像单

个恒星那样大小有别，同一类型的星系是同样大小的。如果所有

的人都是一样高矮，既无侏儒，又无巨人，你就总是可以根据一

个人的视大小来判断出他的远近。这两者是同样的道理。

哈勃用这种方法估计了远方的星系，他得出了在可见（用最

大倍率的望远镜）的空间范围内，星系或多或少均匀地分布的结

论。我们说“或多或少”，是因为在许多地方，星系成群地聚集在

一起，有时竟达上千个之多，就好像许多恒星聚成银河系那样

挤在一起。

我们的这个星系——银河系——看来显然是属于一个比较小

的星系群的，它的成员包括 3 个旋涡状星系（包括银河系和仙女

座星云）、6 个椭球状星系及 4 个不规则星云（其中有两个是大、

小麦哲伦星云）。

不过，除了这种偶而存在的群聚现象外，从帕洛马山天文台

的 200 英寸望远镜看去，星系是相当均匀地散布在 10 亿光年的可

见距离内的，两个相邻星系的平均距离为 500 万光年，在可见的

宇宙地平线上，包容有几十亿个恒星世界！

如果还采用前面用过的比喻，把帝国大厦看作细菌那么大，

地球是颗豌豆，太阳是个南瓜，那么，银河系就是分布在木星轨

247

20&世纪科普经典特藏 从一到无穷大

道范围内的几十亿个南瓜，而许许多多这样的南瓜堆又分布在半

径略小于从地球到最近的恒星这样一个球形空间内。是啊！实在

难找出一种表示宇宙间各种距离所成比例的尺度来啊！瞧，即使

把地球比成一颗豌豆，已知宇宙的大小还是个天文数字！我们试

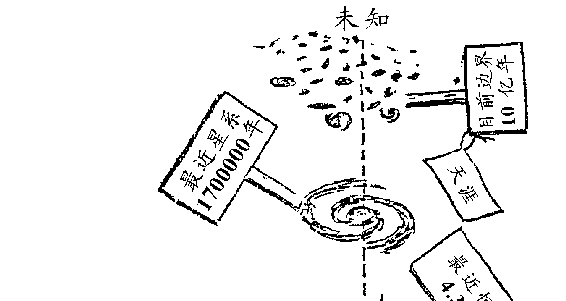
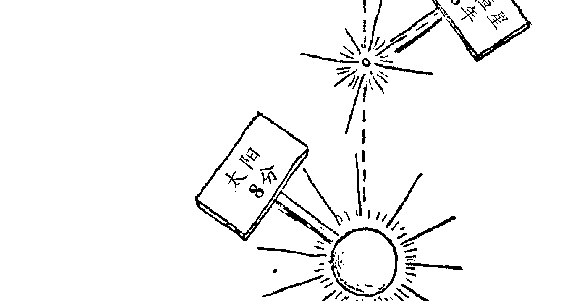
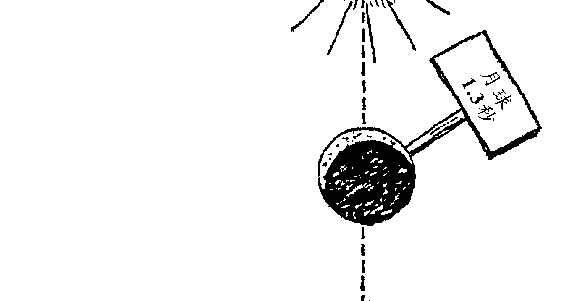
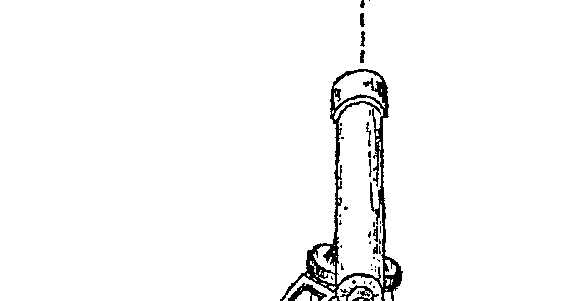
图用图 116 告诉大家，天文学家们是如何一步步地勘测宇宙的：

从地球开始到月亮，然后是太阳、恒星，然后是遥远的星系，一

直到未知世界的边界。

现在，我们准备来解答宇宙的大小这个根本问题。宇宙是无

限伸展的？还是有限的（虽然相当大）体积？随着望远镜越制越

大，越造越精密，我们探询的目光到底是总能发现一些新的、未

被勘查过的空间呢，还是与此相反，我们终将至少在理论上审视

到最后一颗恒星呢？

当我们说宇宙可能是有“确定大小”的时候，当然并不是想

告诉大家，在远到几十亿光年的地方，人们会碰到一堵大墙，上

面写着“此路不通”的字样。

事实上，我们在第三章里已经讲过，空间可以是有限而没有

边界的。这是因为它可以是弯曲的，并且“自我封闭”起来。这

样，一位假想中的空间探险家，尽管他笔直地驾驶着飞船，却会

在空间描出一条短程线，并回到他出发的地方来。

这当然就像是一个古希腊探险者， 从他的家乡雅典城出发一

直向西走，结果在走了许久之后，却发现自己从东门进了这座城

一样。

正如同我们无需周游世界，只凭在一块相对来说很小的部位

上搞搞几何测量，就可以测定地球的曲率一样，我们也可以在现

有望远镜的视程内，测定出宇宙三维空间的曲率。在第五章中，

我们曾看到，有两种不同的曲率：相应于有确定体积的闭空间的

正曲率，和相应马鞍形无限开空间的负曲率（参看图 42）。这两

种空间的区别在于：均匀散布在闭空间内的物体，其数目的增长

慢于距离的立方；而在开空间内则恰恰相反。

248

第十章 不断扩展的视野

图 116 勘测宇宙的里程碑距离是用光年表示的

宇宙空间内“均匀散布的物体”就是各个星系。因此，要想

解决宇宙曲率的问题，只需统计不同距离内单个星系的数目就行

了。

哈勃曾作了这种实际统计，他发现，星系的数目很可能比距

离的立方增长得慢一些，因此，宇宙大概是个有确定体积的正曲

249

20&世纪科普经典特藏 从一到无穷大

率空间。不过一定要记住，哈勃所观察到这种效应非常不显著，

只是在威尔逊山上那架 100 英寸望远镜视线的尽头才刚刚有所觉

察。至于用帕洛马山上那架新的 200 英寸反射式望远镜在最近进

行的最新观测，还没有对这个重大问题作出更明确的答复来。

现在还不能对宇宙是否有限这个问题作出肯定回答的原因还

在于：远处星系的距离只能靠它们的视亮度来确定（根据平方反

比定律）。使用这个方法，需要假设所有的星系都具有同样的亮

度。然而。如果星系的亮度随时变化（即与年代有关），就会导

致错误的结论。要知道，通过帕洛马山望远镜所看到的最近的星

系，大多都在 10 亿光年的远处，因此我们看到的是它们在 10 亿

年前的状况。如果星系随着自己的衰老而变暗（大概是由于有些

活动的恒星成员熄灭所致），那就得对哈勃的结论进行修正。事

实上，只要星系的光度在 10 亿年里（它们寿命的 1/7 左右）改

变一个很小的百分数，就会把宇宙有限这个结论颠倒过来。

因此，大家都看到了，为了确定我们的宇宙到底是有限的还

是无限的，还有许许多多的工作等待我们去做哩！

250