第一章 大 数
一、你能数到多少?
有这么一个故事,说的是两个匈牙利贵族决定做一次数数游戏——谁说出的数字大谁赢。
“好,”一个贵族说,“你先说吧!”
另一个绞尽脑汁想了好几分钟,最后说出了他所想到的最大数字:“3”。
现在轮到第一个动脑筋了。苦思冥想了一刻钟以后,他表示弃权说:“你赢啦!”
这两个贵族的智力当然是不很发达的。再说,这很可能只是一个挖苦人的故事而已。然而,如果上述对话是发生在原始部族
中,这个故事大概就完全可信了。有不少非洲探险家证实,在某些原始部族里,不存在比 3 大的数词。如果问他们当中的一个人有几个儿子,或杀死过多少敌人,那么,要是这个数字大于 3,他就会回答说“许多个。”因此,就计数这项技术来说,这些部族的勇士们可要败在我们幼儿园里的娃娃们的手下了,因为这些娃娃们竟有一直数到十的本领呢!
现在,我们都习惯地认为,我们想把某个数字写成多大,就能写得多大——战争经费以分为单位来表示啦,天体间的距离用英寸来表示啦,等等——只要在某个数字的后面接上一串零就是了。
你可以一直这样写下去,直到手腕发酸为止。这样,尽管目前已知的宇宙&①中所有原子的数目已经很大,等于 300 000 000 000 000 000
① 这是指目前用最大的望远镜所能探测到的那部分宇宙。
2

000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
000 000 000,但是,你还可以写出比这更大的数目来。
上面这个数可以改写得短一些,即写成
3×1074,
在这里,10 的右上角的小号数字 74 表示应该写出多少个零。换句
话说,这个数字意味着 3 要用 10 乘上 74 次。
但是在古代,人们并不知道这种简单的“算术简示法”。这种方法是距今不到两千年的某个佚名的印度数学家发明的。在这个
伟大发明——这确实是一项伟大的发明,尽管我们一般意识不到这一点——出现之前,人们对每个数位上的数字,是用专门的符号反复书写一定次数的办法来表示的。例如,数字 8732 在古埃及人写来是这样的:
而在凯撒(Julius Caeser)*的衙门里,他的办事员会把这个数字写成
MMMMMMMMDCCXXXII
这后一种表示法你一定比较熟悉,因为这种罗马数字直到现在还有些用场——表示书籍的卷数或章数啦,各种表格的栏次啦,
等等。不过,古代的计数很难得超过几千,因此,也就没有发明比一千更高的数位表示符号。一个古罗马人,无论他在数学上是何等训练有素,如果让他写一下“一百万”,他也一定会不知所措。
他所能用的最好的办法,只不过是接连不断地写上一千个 M,这可要花费几个钟点的艰苦劳动啊(图 1)。在古代人的心目中,那些很大的数目字,如天上星星的颗数、海里游鱼的条数、沙滩上沙子的粒数等等,都是“不计其数”,就
像“5”这个数字对原始部族来说也是“不计其数”,只能说成
* 凯撒(公元前 100~前 44 年)是古罗马帝国的统治者。——译者
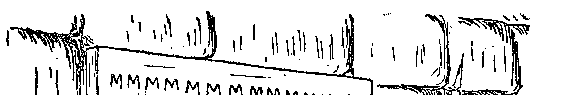




图 1 凯撒时代的一个古罗马人试图用罗马数字来写“一百万”,墙上挂的那块板恐怕连“十万”也写不下“许多”一样。
阿基米德(Archimedes),公元前 3 世纪大名鼎鼎的大科学家,
曾经开动他那出色的大脑,想出了书写巨大数字的方法。在他的
论文《计沙法》中这样写着:
有人认为,无论是在叙拉古&*,还是在整个西西里岛,或
者在世界所有有人烟和无人迹之处,沙子的数目是无穷大的。
也有人认为,这个数目不是无穷大的,然而想要表达出比地
球上沙粒数目还要大的数字是做不到的。很明显,持有这种
观点的人会更加肯定地说,如果把地球想像成一个大沙堆,
并在所有的海洋和洞-穴-里装满沙子,一直装到与最高的山峰
相平,那么,这样堆起来的沙子的总数是无法表示出来的。但
是,我要告诉大家,用我的方法,不但能表示出占地球那么大
地方的沙子的数目,甚至还能表示出占据整个宇宙空间的沙
子的总数。
阿基米德在这篇著名的论文中所提出的方法,同现代科学中
表达大数目字的方法相类似。他从当时古希腊算术中最大的数
* 叙拉古是古代的城市国家,位于意大利西西里岛东南部。——译者
“万”开始,然后引进一个新数“万万”(亿)作为第二阶单位,
然后是“亿亿”(第三阶单位)、“亿亿亿”(第四阶单位),等等。
写个大数字,看来似乎不足挂齿,没有必要专门用几页的篇
幅来谈论。但在阿基米德那个时代,能够找到写出大数字的办法,
确实是一项伟大的发现,使数学向前迈出了一大步。
为了计算填满整个宇宙空间所需的沙子总数,阿基米德首先
得知道宇宙的大小。按照当时的天文学观点,宇宙是一个嵌有星
星的水晶球。阿基米德的同时代人,著名的天文学家,萨摩斯&*
的阿里斯塔克斯(Aristarchus)&**求得从地球到天球面的距离为
10 000 000 000 斯塔迪姆&①,即约为 1 000 000 000 英里。
阿基米德把天球和沙粒的大小相比,进行了一系列足以把小
学生吓出梦魇症来的运算,最后他得出结论说:
很明显,在阿里斯塔克斯所确定的天球内所能装填的沙
子粒数,不会超过一千万个第八阶单位&②。
这里要注意,阿基米德心目中的宇宙的半径要比现代科学家
们所观察到的小得多。十亿英里,这只不过刚刚超过从太阳到土
星 的 距 离 。 以 后 我 们 将 看 到 , 在 望 远 镜 里 , 宇 宙 的 边 缘 是 在
5 000 000 000 000 000 000 000 英里的地方,要填满这样一个已被
观测到的宇宙,所需要的沙子数超过
10100 粒(即 1 的后面有 100 个零)。
这个数字显然比前面提到的宇宙间的原子总数 3×1074 大多了,
这是因为宇宙间并非塞-满了原子。实际上,在一立方米的空间内,
* 萨摩斯是希腊的一个岛。——译者
** 阿里斯塔克斯是公元前 3 世纪的希腊天文学家。——译者
① 斯塔迪姆是古希腊的长度单位,1 斯塔迪姆为 606 英尺 6 英寸,或 188 米。
② 用我们现在的数学表示法,这个数字是:
一千万 第二阶 第三阶 第四阶
(10 000 000)×(100 000 000)×(100 000 000)×(100 000 000)×
第五阶 第六阶 第七阶 第八阶
(100 000 000)×(100 000 000)×(100 000 000)×(100 000 000)
也可以简写成
1063(即在 1 的后面有 63 个零)。


平均才只有一个原子。
要想得到大数目字,并不一定要把整个宇宙倒满沙子,或进
行诸如此类的剧烈活动。事实上,在很多乍一看来似乎很简单的
问题中,也常会遇到极大的数字,尽管你原先决不会想到,其中会
出现大于几千的数字。
有一个人曾经在大数目字上吃了亏,那就是印度的舍罕王
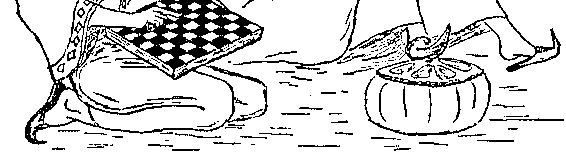
(Shirham)。根据古老的传说,舍罕王打算重赏象棋&*的发明人
和进贡者,宰相西萨·班·达依尔(Sissa Ben Dahir)。这位聪
明大臣的胃口看来并不大,他跪在国王面前说:“陛下,请您
在这张棋盘的第一个小格内,赏给我一粒麦子;在第二个小格
内给两粒,第三格内给四粒,照这样下去,每一小格内都比前
一小格加一倍。陛下啊,把这样摆满棋盘上所有 64 格的麦粒,
都赏给您的仆人罢!”
“爱卿。你所求的并不多啊。”国王说道,心里为自己对这样
一件奇妙的发明所许下的慷慨赏诺不致破费太多而暗喜。
“你当然
会如愿以偿的。”说着,他令人把一袋麦子拿到宝座前。
计数麦粒的工作开始了。第一格内放一粒,第二格内放两粒,
图 2 机敏的数学家西萨·班·达依尔宰相正在向印度的舍罕王请求赏赐
* 这里的象棋指的是国际象棋。整个棋盘是由 64 个小方格组成的正方形。双方的
棋子(每方 16 个,包括王一枚,王后一枚、相两枚、马两枚,车两枚、兵八枚)在
格内移动,以消灭对方的王为胜。棋盘的形状可参见插图 2。——译者
第三格内放四粒,……还没到第二十格,袋子已经空了。一袋又
一袋的麦子被扛到国王面前来。但是,麦粒数一格接一格地增长
得那样迅速,很快就可以看出,即便拿来全印度的粮食,国王也
兑 现 不了 他对西萨·班·达依尔许下 的诺言 了,因 为这需要 有
18 446 744 073 709 551 615 颗麦粒&①呀!
这个数字不像宇宙间的原子总数那样大,不过也已经够可观
了。1 蒲式耳&*小麦约有 5 000 000 颗,照这个数,那就得给西萨·
班·达依尔拿来 4 万亿蒲式耳才行。这位宰相所要求的,竟是全世
界在 2000 年内所生产的全部小麦!
这么一来,舍罕王发觉自己欠了宰相好大一笔债。什么办?要
么是忍受西萨·班·达依尔没完没了的讨债,要么是干脆砍掉他
的脑袋。据我猜想,国王大概选择了后面这个办法。
另一个由大数目字当主角的故事也出自印度,它是和“世界
末日”的问题有关的。偏爱数学的历史学家鲍尔(Ball)是这样讲
述这段故事的&②:
在世界中心贝拿勒斯&**的圣庙里。安放着一个黄铜板,
板上插着三根宝石针。每根针高约 1 腕尺(1 腕尺大约合 20
英寸)。像韭菜叶那样粗细。梵天&***在创造世界的时候,在
其中的一根针上从下到上放下了由大到小的 64 片金片。这就
是所谓梵塔。不论白天黑夜,都有一个值班的僧侣按照梵天
① 这位聪明的宰相所要求的麦子粒数可写为
1+2+22+23+24+……262+263
在数学上,这类每一个数都是前一个数的固定倍数的数列叫做几何级数(在我们这个例子
里,这个倍数为 2)。可以证明,这种级数所有各项之和,等于固定倍数(在本例中为 2)
的项数次方幂(在本例中为 64)减去第一项(此例中为 1)所得到的差除以固定倍数与 1
之差。这就是:
64
2 −1
64
= 2 −1
2 −1
直接写出结果来就是
18 446 744 073 709 551 615。
* 蒲式耳是欧美的容量单位(计算谷物专用)。1 蒲式耳约合 35.2 升。——译者
② 引自 W.W.R.Ball,&Mathmatical Recreations and Essays(《数学拾零》)。
** 贝拿勒斯是佛教的圣地,位于印度北部。——译者
*** 梵天是印度教的主神。——译者
7





20&世纪科普经典特藏 从一到无穷大
不渝的法则,把这些金片在三根针上移来移去:一次只能移
一片,并且要求不管在哪一根针上,小片永远在大片的上面。
当所有 64 片都从梵天创造世界时所放的那根针上移到另外一
根针上时,世界就将在一声霹雳中消灭,梵塔、庙宇和众生都
将同归于尽。
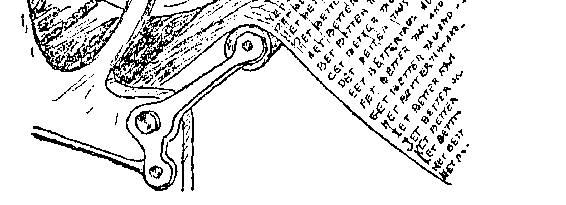
图 3 是按故事的情节所作的画,只是金片少画了一些。你不妨
用纸板代表金片,拿长钉代替宝石针,自己搞这么一个玩具。不难
图 3 一个僧侣在大佛像前解决“世界未日”的问题。为了
省事起见,这里没有画出 64 片金片来
发现,按上述规则移动金片的规律是:不管把哪一片移到另一根
针上,移动的次数总要比移动上面一片增加一倍。第一片只需一
次,下一片就按几何级数加倍。这样,当把第 64 片也移走后,总
的移动次数便和西萨·班·达依尔所要求的麦粒数一样多了&①!
把这座梵塔全部 64 片金片都移到另一根针上,需要多长时间
① 如果只有 7 片,则需要移动的次数为
1+21+22+23+……=27-1=2×2×2×2×2×2×2-1=127
当金片为 64 片时,需要移动的次数则为
264-1=18 446 744 073 709 551 615。
这就和西萨·班·达依尔所要求的麦粒数相同了。
8
第一章 大 数
呢?一年有 31 558 000 秒。假如僧侣们每一秒钟移动一次,日夜不
停,节假日照常干,也需要将近 5800 亿年才能完成。
把这个纯属传说的寓言和按现代科学得出的推测对比一下倒
是很有意思的。按照现代的宇宙进化论,恒星、太阳、行星(包
括地球)是在大约 30 亿年前由不定形物质形成的。我们还知道,
给恒星,特别是给太阳提供能量的“原子燃料”还能维持 100 亿
~150 亿年(见“创世的年代”一章)。因此,我们太阳系的整个
寿命无疑要短于 200 亿年,而不像这个印度传说中所宣扬的那样
长!不过,传说毕竟只是传说啊!
在文学作品中所提及的最大数字,大概就是那个有名的“印
刷行数问题”了。
假设有一台印刷机器可以连续印出一行行文字,并且每一行
都能自动换一个字母或其他印刷符号,从而变成与其他行不同的
字母组合。这样一架机器包括一组圆盘,盘与盘之间像汽车里程
表那祥装配,盘缘刻有全部字母和符号。这样,每一片轮盘转动一
周,就会带动下一个轮盘转动一个符号。纸张通过滚筒自动送入
盘下。这样的机器制造起来没有太大的困难,图 4 是这种机器的示
意图。
现在,让我们开动这架印刷机,并检查印出的那些没完没了
的东西吧。在印出的一行行字母组合当中,大多数根本没有什么意
思,如:
aaaaaaaaaaaa…
或者
boobooboobooboo…
或者
zawkpopkossscilm…
但是,既然这台机器能印出所有可能的字母及符号的组合,我们就
能从这堆玩艺儿中找出有点意思的句子。当然,其中又有许多是
胡说八道,如:
9


20&世纪科普经典特藏 从一到无穷大
图 4 一台刚刚印出一行莎士比亚诗句的自动印刷机
horse has six legs and…(马有六条腿,并且……)
或者
I like apples cooked in terpentin…
(我喜欢吃松节油煎苹果……)。
不过, 只要找下去, 一定会发现莎士比亚(William Shake-
spare)*的每一行著作,甚至包括被他扔进废纸篓里去的句子!
实际上,这台机器会印出人类自从能够写字以来所写出的一
切句子:每一句散文,每一行诗歌,每一篇社论,每一则广告,每
一卷厚厚的学术论文,每一封书信,每一份订奶单……
不仅如此,这架机器还将印出今后各个世纪所要印出的东西。
从滚筒下的纸卷中,我们可以读到 30 世纪的诗章,未来的科学发
现,2344 年星际交通事故的统计,还有一篇篇尚未被作家们创作
出来的长、短篇小说。出版商们只要搞出这么一台机器,把它安装
在地下室里,然后从印出的纸卷里寻找好句子来出版就是了——
他们现在所干的不也差不多就是这样嘛!
为什么人们没有这样干呢?
* 莎士比亚(1564~1616 年),文艺复兴时代的著名英国剧作家及诗人。——译者
10
第一章 大 数
来,让我们算算看,为了得到所有字母和印刷符号的组合,该
印出多少行来。
英语中有 26 个字母、十个数码(0,1,2,…,9)、还有 14
个常用符号(空白、句号、逗号、冒号、分号、问号、惊叹号、
破折号、连字符、引号、省略号、小括号、中括号、大括号),共
50 个字符。再假设这台机器有 65 个轮盘,以对应每一印刷行的平
均字数。印出的每一行中,排头的那个字符可以是 50 个字符当中
的任何一个,因此有 50 种可能性。对这 50 种可能性当中的每一
种,第二个字符又有 50 种可能性,因此共有 50×50=2 500 种。对
于这前两个字符的每一种可能性,第三个字符仍有 50 种选择。这
样下去,整行进行安排的可能性的总数等于
65 个
50×50×50×…×50
或者 5065,即等于 10110。
要想知道这个数字有多么巨大,你可以设想宇宙间的每个原
子都变成一台独立的印刷机,这样就有 3×1074 部机器同时工作。
再假定所有这些机器从地球诞生以来就一直在工作,即它们已经
工作了 30 亿年或 1017 秒。你还可以假定这些机器都以原子振动的
频率进行工作,也就是说,一秒钟可以印出 1015 行。那么,到目前
为止,这些机器印出的总行数大约是
3×1074×1017×1015=3×10106,
这只不过是上述可能性总数的三千分之一左右而已。
看来,想要在这些自动印出的东西里面挑选点什么,那确实
得花费非常非常长的时间了!
二、怎样计数无穷大的数字
上一节我们谈了一些数字,其中有不少是毫不含糊的大数。
但是这些巨大的数字,例如西萨·班·达依尔所要求的麦子粒数,
虽然大得难以令人置信,但毕竟还是有限的,也就是说,只要有足
11
20&世纪科普经典特藏 从一到无穷大
够的时间,人们总能把它们从头到尾写出来。
然而,确实存在着一些无穷大的数,它们比我们所能写出的
无论多长的数都还要大。例如,
“所有整数的个数”和“一条线上
所有几何点的个数”显然都是无穷大的。关于这类数字,除了说
它们是无穷大之外,我们还能说什么呢?难道我们能够比较一下
上面那两个无穷大的数,看看哪个“更大些”吗?
“所有整数的个数和一条线上所有几何点的个数,究竟哪个大
些?”——这个问题有意义吗?乍一看,提这个问题可真是头脑发
昏,但是著名数学家康托尔(Georg Cantor)首先思考了这个问
题。因此,他确实可被称为“无穷大数算术”的奠基人。
当我们要比较几个无穷大的数的大小时,就会面临这样一个
问题:这些数既不能读出来,也无法写出来,该怎样比较呢?这下
子,我们自己可有点像一个想要弄清自己的财物中,究竟是玻璃
珠子多,还是铜币多的原始部族人了。你大概还记得,那些人只能
数到 3。难道他会因为数不清大数而放弃比较珠子和铜币数目的打
算?根本不会如此。如果他足够聪明,他一定会通过把珠子和铜币
逐个相比的办法来得出答案。他可以把一粒珠子和一枚铜币放在
一起,另一粒珠子和另一枚铜币放在一起,并且一直这样做下去。
如果珠子用光了,而还剩下些铜币,他就知道,铜币多于珠子;如
果铜币先用光了,珠子却还有多余,他就明白,珠子多于铜币;如
果两者同时用光,他就晓得,珠子和铜币数目相等。
康托尔所提出的比较两个无穷大数的方法正好与此相同:我
们可以给两组无穷大数列中的各个数一一配对。如果最后这两组
都一个不剩,这两组无穷大就是相等的;如果有一组还有些数没
有配出去,这一组就比另一组大些,或者说强些。
这显然是合理的、并且实际上也是唯一可行的比较两个无穷
大数的方法。但是,当你把这个方法付诸实施时,你还得准备再吃
一惊。举例来说,所有偶数和所有奇数这两个无穷大数列,你当然
会直觉地感到它们的数目相等。应用上述法则,也完全合理,因为
12
第一章 大 数
这两组数间可建立如下的一一对应关系:
1 3 5 7 9 11 13 15 17 19 等等
2 4 6 8 10 12 14 16 18 20 等等
在这个表中,每一个偶数都与一个奇数相对应。看,这确实再
简单、再自然不过了!
但是,且慢。你再想一想:所有整数(奇偶数都在内)的数
目和单单偶数的数目,哪个大呢?当然,你会说前者大一些,因为
所有的整数不但包含了所有的偶数,还要加上所有的奇数啊。但
这只不过是你的印象而已。只有应用上述比较两个无穷大数的法
则,才能得出正确的结果。如果你应用了这个法则,你就会吃惊地
发现,你的印象是错误的。事实上,下面就是所有整数和偶数的一
一对应表:
1 2 3 4 5 6 7 8 等等
2 4 6 8 10 12 14 16 等等
按照上述比较无穷大数的规则,我们得承认,偶数的数目正
好和所有整数的数目一样大。当然,这个结论看来是十分荒谬的,
因为偶数只是所有整数的一部分。但是不要忘了,我们是在与无
穷大数打交道,因而就必须做好遇到异常的性质的思想准备。
在无穷大的世界里,部分可能等于全部!关于这一点,著名德
国数学家希尔伯特(David Hilbert)有一则故事说明的再好不过
了。据说在他的一篇讨论无穷大的演讲中,他曾用下面的话来叙
述无穷大的似非而是的性质:①
我们设想有一家旅店,内设有限个房间,而所有的房间都已
客满。这时来了位新客,想订个房间。旅店主说:“对不起,所
有的房间都住满了。”现在再设想另一家旅店,内设无限多个房
① 这段文字从未印行过,甚至希尔伯特本人也未写成文字,但是广泛流传着。本书引
自 R. Courant,&The Complete Collection of Helbert Stories。
13
20&世纪科普经典特藏 从一到无穷大
间,所有房间也都客满了。这时也有一位新客来临,想订个房间。
“不成问题!”旅店主说。接着,他就把一号房间里的旅客移
至二号房间,二号房间的旅客移到三号房间,三号房间的旅客移
到四号房间,等等,这一来,新客就住进了已被腾空的一号房
间。
我们再设想一座有无限个房间的旅店,各个房间也都住满
了。这时,又来了无穷多位要求订房间的客人。
“好的,先生们请等一会儿。”旅店主说。
他把一号房间的旅客移到二号房间,二号房间的旅客移到四
号房间,三号房间的旅客移到六号房间,如此,如此。
现在,所有的单号房间都腾出来了。新来的无穷多位客人可
以住进去了。
由于希尔伯特讲这段故事时正值世界大战期间,所以,即使
在华盛顿,这段话也不容易被人们所理解&*。但这个例子却确实举
到了点子上,它使我们明白了:无穷大数的性质与我们在普通算
术中所遇到的一般数字大不一样。
按照比较两个无穷大数的康托尔法则,我们还能证明,所有
的普通分数 ⎛
3 375
⎞
⎜ 如 ,
等⎟ 的数目和所有的整数相同。把所有的分
⎝
7 8
⎠
数按照下述规则排列起来:先写下分子与分母之和为 2 的分数,这
样的分数只有一个,即 1 ;然后写下两者之和为 3 的分数,即 2 和
1
1
1 ;再往下是两者之和为 4 的,即 3 , 2 , 1 。这样做下去,我们
2
1
2
3
可以得到一个无穷的分数数列,它包括了所有的分数(图 5)。现
在,在这个数列旁边写上整数数列,就得到了无穷分数与无穷整
数的一一对应。可见,它们的数目又是相等的!
* 作者这句话说得比较含蓄,意思大概是说:本来这些概念就不好懂,再加上希尔伯
特的国籍是德国——美国在世界大战中的敌国,因此,这段话当时就更不易为美国人所接
受了。——译者
14


第一章 大 数
图 5 原始人和康托尔教授都在比较他们数不出来的数目的大小
你可能会说“是啊,这一切都很妙,不过,这是不是就意味
着,所有的无穷大数都是相等的呢?如果是这样,那还有什么可比
的呢?”
不。事情并不是这样。人们可以很容易地找出比所有整数或
所有分数所构成的无穷大数还要大的无穷大数来。
如果研究一下前面出现过的那个比较一条线段上的点数和整数
的个数的多少的问题,我们就会发现,这两个数目是不一样大
的。线段上的点数要比整数的个数多得多。为了证明这一点,我们
先来建立一段线段(比如说 1 寸长)和整数数列的一一对应关系。
这条线段上的每一点都可用这一点到这条线的一端的距离来
表示,而这个距离可以写成无穷小数的形式,如
0.735 062 478 005 6……
或者
0.382 503 756 32……①
现在我们所要做的,就是比较一下所有整数的数目和所有可能存
① 我们已经假定线段长 1 寸,因此这些小数都小于 1。
15
20&世纪科普经典特藏 从一到无穷大
在的无穷小数的数目。那么,上面写出的无穷小数和 3 , 8 这类
7
277
分数有什么不同呢?
大家一定还记得在算术课上学过的这样一条规则:每一个普
2
·
通分数都可以化成无穷循环小数。如 = 0.6666……=0.66, 3 =
3
7
0.428571⋰428571⋰428571⋰4
·
·
……=0.428571。我们已经证明过,
所有分数的数目和所有整数的数目相等,所以,所有循环小数的数
目必定与所有整数的数目相等。但是,一条线段上的点不可能完
全由循环小数表示出来。绝大多数的点是由不循环的小数表示的。
因此就很容易证明,在这种情况下,一一对应关系是无法建立的。
假定有人声称他已经建立了这种对应关系,并且,对应关系
具有如下形式:
N
1 0. 3 8 6 0 2 5 6 3 0 7 8……
2 0. 5 7 3 5 0 7 6 2 0 5 0……
3 0. 9 9 3 5 6 7 5 3 2 0 7……
4 0. 2 5 7 6 3 2 0 0 4 5 6……
5 0. 0 0 0 0 5 3 2 0 5 6 2……
6 0. 9 9 0 3 5 6 3 8 5 6 7……
7 0. 5 5 5 2 2 7 3 0 5 6 7……
8 0. 0 5 2 7 7 3 6 5 6 4 2……
· ……………………………
· ……………………………
· ……………………………
当然,由于不可能把无穷多个整数和无穷多个小数一个不漏
地写光,因此,上述声称只不过意味着此人发现了某种普遍规律
(类似于我们用来排列分数的规律),在这种规律的指导下,他制
定了上表,而且任何一个小数或迟或早都会在这张表上出现。
16
第一章 大 数
不过,我们很容易证明,任何一个这类的声称都是站不住脚
的,因为我们一定还能写出没有包括在这张无穷表格之中的无穷多
个小数。怎么写呢?再简单不过了。让这个小数的第一小数位
(十分位)不同于表中第一号小数的第一小数位,第二小数位(百
分位)不同于表中第二号小数的第二小数位,等等。这个数可能
就是这个样子(还可能是别的样子):
非 3 非 7 非 3 非 6 非 5 非 6 非 3 非 5 等等
0 . 5 2 7 4 0 7 1 2
这个数无论如何在上表中是找不到的。如果此表的作者对
你说,你的这个数在他那个表上排在第 137 号(或其他任何一
号),你就可以立即回答说:“不,我这个数不是你那个数,因为
这个数的第 137 小数位和你那个数的第 137 小数位不同。”
这么一来,线上的点和整数之间的一一对应就建立不起来了。
也就是说,线上的点数所构成的无穷大数大于(或强于)所有整数
或分数所构成的无穷大数。
刚才所讨论的线段是“1 寸长”。不过很容易证明,按照“无
穷大数算术”的规则,不管多长的线段都是一样。事实上,1 寸长
的线段也好,1 尺长的线段也好,1 里长的线段也好,上面的点数都
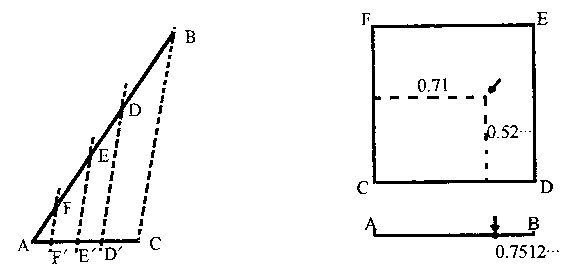
是相同的。只要看看图 6 即可明了,&AB&和&AC&为不同长度的两条线
段,现在要比较它们的点数。过&AB&的每一个点作&BC&的平行线,
都会与&AC&相交,这样就形成了一组点。如&D&与&D′,&E&与&E′,&F&与
F′等。对&AB&上的任意一点,&AC&上都有一个点和它相对应,反之亦
然。这样,就建立了一一对应的关系。可见,按照我们的规则,这
两个无穷大数是相等的。
通过这种对无穷大数的分析,还能得到一个更加令人惊异的
结论:平面上所有的点数和线段上所有的点数相等。为了证明这一
点,我们来考虑一条长 1 寸的线段&AB&上的点数和边长 1 寸的正方
形&CDEF&上的点数(图 7)。
17
20&世纪科普经典特藏 从一到无穷大
图 6 图 7
假定线段上某点的位置是 0.75120386…。我们可以把这个数
按奇分位和偶分位分开,组成两个不同的小数:
0 . 7 1 0 8…
和
0 . 5 2 3 6…
以这两个数分别量度正方形的水平方向和垂直方向的距离,便得
出一个点,这个点就叫做原来线段上那个点的“对偶点”。反过
来,对于正方形内的任意一点,比如说由 0.4835…和 0.9907…这
两个数描述的点,我们把这两个数掺到一起,就得到了线段上的
相应的“对偶点”0.49893057…。
很清楚,这种做法可以建立那两组点的一一对应关系。线段上
的每一个点在平面上都有一个对应的点,平面上的每一个点在线段
上也有一个对应点,没有剩下来的点。因此,按照康托尔的标准,
正方形内所有点数所构成的无穷大数与线段上点数的无穷大数相等。
用同样的方法,我们也容易证明,立方体-内所有的点数和正
方形或线段上的所有点数相等,只要把代表线段上一个点的无穷
小数分作三部分&①,并用这三个新小数在立方体-内找“对偶点”就
① 例如,我们可把数字
0 . 7 3 5 1 0 6 8 2 2 5 4 8 3 1 2……
分成下列三个新的小数:
0 . 7 1 8 5 3…,
0 . 3 0 2 4 1…,
0 . 5 6 2 8 2…。
18

行了。和两条不同长度线段的情况一样,正方形和立方体-内点数
的多少与它们的大小无关。
尽管几何点的个数要比整数和分数的数目大,但数学家们还
知道比它更大的数。事实上,人们已经发现,各种曲线,包括任何
一种奇形怪状的样式在内,它们的样式的数目比所有几何点的数目还
要大。因此,应该把它看作是第三级无穷数列。
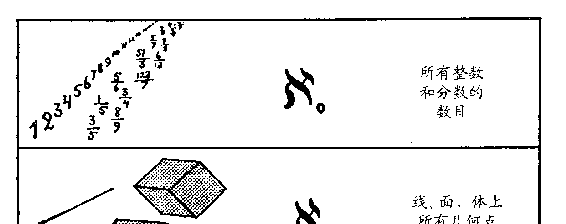
按照“无穷大数算术”的奠基者康托尔的意见,无穷大数是
用希伯来字母ℵ(读作阿莱夫)表示的,在字母的右下角,再用一
个小号数字表示这个无穷大数的级别。这样一来,数目字(包括
无穷大数)的数列就成为
1,2,3,4,5,…ℵ1,ℵ2,ℵ3…
我们说“一条线段上有ℵ1 个点”或“曲线的样式有ℵ2 种”,就和我们平常说“世界有 7 大洲”或“一副扑克牌有 54 张”一样简单了。
图 8 无穷大数的头三级
在结束关于无穷大数的讨论时,我们要指出,无穷大数的级
只要有几个,就足够把人们所能想像出的任何无穷大数都包括进去了。大家知道,ℵ0 表示所有整数的数目,ℵ1 表示所有几何点的
数目,ℵ2 表示所有曲线的数目,但到目前为止,还没有人想得出
一种能用ℵ3 来表示的无穷大数来。看来,头三级无穷大数就足以
包括我们所能想到的一切无穷大数了。因此,我们现在的处境,正
好跟我们前面的原始部族人相反:他有许多个儿子,可却数不过
3;我们什么都数得清,却又没有那么多东西让我们来数!