第二章自然数和人工数

一、最纯粹的数学

数学往往被人们、特别是被数学家们奉为科学的皇后。贵为

皇后，它当然不能屈尊俯就其他学科。因此，在一次“纯粹数学

和应用数学联席会议”上，当有人邀请希尔伯特作一次公开演讲，

以求消除存在于这两种数学家之间的敌对情绪时，他这样说：

经常听到有人说，纯粹数学和应用数学是互相对立的。这是

不符合事实的，纯粹数学和应用数学不是互相对立的。它们过去

不曾对立过，将来也不会对立。它们是对立不起来的，因为在事

实上它们两者毫无共同之处。

然而，尽管数学喜欢保持自己的纯粹性，并尽力远离其他学

科，其他学科却一直打算尽量同数学“亲善”，特别是物理学。事

实上，纯粹数学的几乎每一个分支，包括诸如抽象群、不可逆代

数、非欧几何等一向被认为纯而又纯、决不能派任何用场的数学

理论，现在也都已被用来解释物质世界的这个性质或那个性质了。

但是，迄今为止，数学还有一个大分支没找到什么用途（除

了起智力体操的作用以外），它真可以戴上“纯粹之王冠”哩。这

就是所谓“数论”（这里的数指整数），它是最古老的一门数学分

支，也是纯粹数学思维的最错综复杂的产物。

说来也怪，数论这门最纯粹的科学，从某种意义上说，又可

以称为经验科学，甚至可称为实验科学。事实上，它的绝大多数定

理都是靠用数字试着干某些事情而建立起来的，正如物理学定律

是靠用物体试着干某些事情而建立起来一样。并且，数论的一些定

20&世纪科普经典特藏从一到无穷大

理已“从数学上”得到了证明，而另一些却还停留在经验的阶段，

至今仍在使最卓越的数学家绞尽脑汁，这一点也和物理学一样。

我们可以用质数问题作为例子。所谓质数，就是不能用两个

或两个以上较小整数的乘积来表示的数，如 1，2，3，5，7，11，

13，17，等等。而 12 可以写成 2×2×3，所以就不是质数。

质数的数目是无穷无尽、没有终极的呢，还是存在一个最大

的质数，即凡是比这个最大质数还大的数都可以表为几个质数

的乘积呢？这个问题是欧几里得（Euclid）*最先想到的，他自己还

作了一个简单而优美的证明，证明没有“最大的质数”，质数数目

的延伸是不受任何限制的。

为了研究这个问题，不妨暂时假设已知质数的个数是有限的，

最大的一个用&N&表示。现在让我们把所有已知的质数都乘起来，

再加上 1。这写成数学式是：

（1×2×3×5×7×11×13×……×&N）+1。

这个数当然比我们所假设的“最大质数”&N&大得多。但是，十分

明显，这个数是不能被到&N&为止（包括&N&在内）的任何一个质数

除尽的，因为从这个数的产生方式就可以看出，拿任何质数来除

它，都会剩下 1。

因此，这个数要么本身也是个质数，要么是能被比&N&还大的

质数整除。而这两种可能性都和原先关于&N&为最大质数的假设相

矛盾。

这种证明方式叫做反证法，是数学家们爱用的工具之一。

我们既然知道质数的数目是无限的，自然就会想问一问，是

否有什么简单方法可以把它们一个不漏地挨个写出来。古希腊的

哲学家兼数学家埃拉托色尼（Eratosthenes）提出了一种名叫“过

筛”的方法。这就是把整个自然数列 1，2，3，4…统统写下来，

然后去掉所有 2 的倍数、3 的倍数、5 的倍数等等。前 100 个数

*&欧几里得（约公元前 330～前 275 年），古希腊几何学家。——译者

第二章

自然数和人工数

“过筛”后的情况如图 9 所示，共剩下 26 个质数。用这种原理简

单的过筛方法，我们已经得到了 10 亿以内的质数表。

图 9

如果能导出一个公式，从而能迅速而自动地推算出所有的质

数（并且仅仅是质数），那该多简便啊。但是，经过了多少世纪的

努力，并没有找到这个公式。1640 年，著名的法国数学家费马

（Pierre Fermat）认为自己找到了一个这样的公式。这个公式是 2

2&n

+ 1，&n&取自然数的各个值 1，2，3，4 等等。

从这个公式我们得到：

2 +1= 5，

2 +1= 17，

2 +1= 257，

2 +1= 65 537。

这几个数都是质数。但在费马宣称他取得这个成就以后一个

20&世纪科普经典特藏从一到无穷大

世纪，德国数学家欧拉（Leonard Euler）指出，费马的第五个数

2 +1 = 4 294 967 297 不是个质数，而是 6 700 417 和 641 的乘积。

因此，费马这个推算质数的经验公式被证明是错的。

还有一个值得一提的公式，用这个公式可以得到许多质数。

这个公式是：

n&2 -&n+41，

其中&n&也取自然数各个值 1，2，3 等等。已经发现，在&n&为 1 到 40

的情况下，用这个公式都能得出质数。但不幸得很，到了第 41 步，

这个公式也不行了。

事实上，

(41)2-41+41＝412＝41×41，

这是一个平方数，而不是个质数。

人们还试验过另一个公式，它是

n&2-79&n+1601，

这个公式在&n&从 1 到 79 时都能得到质数，但当，&n＝80 时，它又不

成立了！

因此，寻找只给出质数的普遍公式的问题至今仍然没有解决。

数论定理的另一个有趣的例子，是 1742 年提出的所谓“哥德

巴赫（Goldbach）猜想”。这是一个迄今既没有被证明也没有被推

翻的定理，内容是：任何一个偶数都能表示为两个质数之和。从一

些简单例子，你很容易看出这句话是对的。例如，12=7+5，24=

17+7，32=29+3。但是数学家们在这方面作了大量工作，却仍然

既不能做出肯定的断语，也不能找出一个反证。1931 年，苏联数

学家史尼雷尔曼（Schnirelman）朝着问题的最终解决迈出了建设

性的第一步。他证明了，每个偶数都能表示为不多于 300 000 个质数

之和。“300 000 个质数之和”和“2 个质数之和”之间的距离，后

来又被另一个苏联数学家维诺格拉多夫（Vinogradoff）大大缩短

了。他把史尼雷尔曼那个结论改成了“4 个质数之和”。但是，从

维诺格拉多夫的“4 个质数”到哥德巴赫的“2 个质数”，这最后

第二章

自然数和人工数

的两步大概是最难走的。谁也不能告诉你，要想最后证明或最后

推翻这个令人作难的猜想，到底是需要几年还是需要几个世纪&*。

可见，谈到推导能自动给出直到任意大的所有质数的公式的

问题，从现在来看，我们离这一步还远得很哩！目前我们甚至连到

底存在不存在这样的公式，也都还没有把握呢！

现在，让我们换个小一点的问题看一看——在给定的范围内

质数所能占的百分比有多大。这个比值是随着数的增长而加大还

是减小，或者是近似为常数呢？我们可以用经验方法，即通过查

找各种不同数值范围内质数数目的方法，来解决这个问题。这

样，我们查出，100 之内有 26 个质数，在 1 000 之内有 168 个，在

1 000 000 之内有 78 498 个，在 1 000 000 000 之内有 50 847 478 个。

把质数个数除以相应范围内的整数个数，得出下表：

数值范围

质数数目

比率

偏差（%）

1～&N

ln&N

1～100

26 0.260

0.217

1～1000

168 0.168

0.145

1～106

78 498

0.078 498

0.072 382

1～109

50 847 478

0.050 847 478

0.048 254 942

从这张表上首先可以看出，随着数值范围的扩大，质数的数

目相对减少了。但是，并不存在质数的终止点。

有没有一个简单方法可以用数学形式表示这种质数比值随范

围的扩大而减小的现象呢？有的，并且，这个有关质数平均分布的

规律已经成为数学上最值得称道的发现之一。这条规律很简单，

就是：从 1 到任何自然数&N&之间所含质数的百分比，近似由&N&的自然

对数&①的倒数所表示。&N&越大，这个规律就越精确。

从上表的第四栏：可以看到&N&的自然对数的倒数。把它们和

前一栏对比一下，就会看出两者是很相近的，并且，&N&越大，它们

* 我国数学家陈景润又把这个结果推进了一步。他的结论是：任何一个偶数都可以表

示为一个质数和不多于两个质数的乘积之和（见《中国科学》，1973 年第二期）。——译者

① 简单地说一个数的自然对数，近似地等于它的一般对数乘以 2.3026。

20&世纪科普经典特藏从一到无穷大

也就越相近。

有许多数论上的定理，开始时都是凭经验作为假设提出，而

在很长一段时间内得不到严格证明的。上面这个质数定理也是如

此。直到 19 世纪末，法国数学家阿达马（Jacques Solomon Had-

amard）和比利时数学家布散（de la Vallée Poussin）才终于证明了

它。由于证明的方法太繁难，我们这里就不介绍了。

既然谈到整数，就不能不提一提著名的费马大数定理，尽管这

个定理和质数没有必然的联系。要研究这个问题，先要回溯到古

埃及。古埃及的每一个好木匠都知道，一个边长之比为 3:4:5 的

三角形中，必定有一个角是直角。现在有人把这样的三角形叫做

埃及三角形。古埃及的木匠就是用它作为自己的三角尺的&①。

公元三世纪，亚历山大里亚城的刁番图（Diophante）*开始考

虑这样一个问题：从两个整数的平方和等于另一整数的平方这一

点来说，具有这种性质的是否只有 3 和 4 这两个整数？他证明了还

有其他具有同样性质的整数（实际上有无穷多组），并给出了求这

些数的一些规则。这类三个边都是整数的直角三角形称为毕达哥

拉斯三角形。简单说来，求这种三角形的三边就是解方程

x&2 +&y&2 =&z&2，

式中，&x，&y，&z必须是整数&②。

① 在初等几何课本中，毕达哥拉斯定理证明了 32 + 42 = 52（这个定理就是我国

古代的勾股定理。——译者）

* 刁番图(210～290 年），古希腊数学家。——译者

② 刁番图的规则是这样的：找两个数&a&和&b，使&2ab&为完全平方。这时，

x&=&a&+ 2&ab&，&y&=&b&+ 2&ab&，&z&=&a&+&b&+ 2&ab&。

用代数方法很容易证明，这时

x&2 +&y&2 =&z&2

用这个方法，我们可以列出所有各种可能性。最前面的几个例子是：

32 + 42 = 52（埃及三角形），

52 + 122 = 132，

62 + 82 = 102，

72 + 242 = 252，

82 + 152 = 172，

92 + 122 = 152，

92 + 402 = 412，

102 + 242 = 262。

第二章

自然数和人工数

1621 年，费马在巴黎买了一本刁番图所著《算术学》的法文

译本，里面提到了毕达哥拉斯三角形。当费马读这本书的时候，他

在书上空白处作一些简短的笔记，并且指出，

x&2 +&y&2 =&z&2

有无穷多组整数解，而形如

xn&+&yn&=&zn

的方程，当&n&大于 2 时，永远没有整数解。

他后来说：

“我当时想出了一个绝妙的证明方法，但是书上的

空白太窄了，写不完。”

费马死后，人们在他的图书室里找到了刁番图的那本书，里

面的笔记也公诸于世了。那是在三个世纪以前。从那个时候以来，

各国最优秀的数学家们都尝试重新作出费马写笔记时所想到的证

明，但至今都没有成功。当然，在这方面已有了相当大的发展，一

门全新的数学分支——“理想数论”——在这个过程中创建起来

了。欧拉证明了，方程

x&3 +&y&3 =&z&3 和&x&4 +&y&4 =&z&4

不可能有整数解。狄里克莱（Peter Gustav Lejeune Dirichlet）*证明

了，&x&5 +&y&5 =&z&5 也是这样。依靠其他一些数学家的共同努力，现在

已经证明，在&n小于 269 的情况下，费马的这个方程都没有整数

解。不过，对指数&n在任何值下都成立的普遍证明，却一直没能作

出&**。人们越来越倾向于认为，费马不是根本没有进行证明，就是

在证明过程中有什么地方搞错了。为征求这个问题的解答，曾经

悬赏过 10 万马克&***。那时，研究这个问题的人真是不少，不过，

这些拜金的业余数学家都一事无成。

这个定理仍然有可能是错误的，只要能找到一个实例，证实

* 狄里克莱（1805～1859 年），德国数学家。——译者

** 费马定理于 1995 年被英国数学家安德鲁·怀尔斯（Andrew Wiles）证明。——责任

编辑

*** 马克，德国钱币名。——译者

20&世纪科普经典特藏从一到无穷大

两个整数的某一次幂的和等于另一个整数的同一次幂的和就行了。不

过，这个幂次一定要在比 269 大的数目中去找，这可不是一件容易

事啊。

二、神秘的

− 1

现在，让我们来搞点高级算术。二二得四，三三见九，四四一

十六，五五二十五，因此，四的算术平方根为二，九的算术平方根是

三，十六的算术平方根是四，二十五的算术平方根是五&①。

然而，负数的平方根是什么样呢？

− 和

− 之类的表式有

什么意义吗？

如果从有理数的角度来揣想这样的数，你一定会得出结论，

说明这样的式子没有任何意义，这里可以引用 12 世纪的一位数学家

拜斯迦罗（Brahmin Bhaskara）*的话：“正数的平方是正数，负

数的平方也是正数。因此，一个正数的平方根是两重的：一个正数

和一个负数。负数没有平方根，因为负数并不是平方数。”

可是数学家的脾气倔强得很。如果有些看起来没有意义的东

西不断在数学公式中冒头，他们就会尽可能创造出一些意义来。

负数的平方根就在很多地方冒过头，既在古老而简单的算术问题

上出现，也在 20 世纪相对论的时空结合问题上露面。

第一个将负数的平方根这个“显然”没有意义的东西写到公

式里的勇士，是 16 世纪的意大利数学家卡尔丹（Cardan）。在讨论

是否有可能将 10 分成两部分，使两者的乘积等于 40 时，他指出，

① 还有其他许多数的平方根也很容易得出。如，

5 ＝2.236…，

因为

（2.236…）×（2.236…）＝5.000…；

7.3 ＝2.702…，

因为

（2.702…）×（2.702…）＝7.3000…。

* 拜斯迦罗（1114～1185 年），印度数学家。——译者

第二章

自然数和人工数

尽管这个问题没有任何有理解，然而，如果把答案写成 5 + −15

和5 − −15 这样两个怪模怪样的表式，就可以满足要求了&①。

尽管卡尔丹认为这两个表式没有意义，是虚构的、想像的，但

是他毕竟还是把它们写下来了。

既然有人敢把负数的平方根写下来，并且，尽管这有点想入

非非，却把 10 分成两个乘起来等于 40 的事办成了；这样，有人开

了头，负数的平方根——卡尔丹给它起了个大号叫“虚数”——

就越来越经常地被科学家们所使用了，虽则总是伴有很大保留，

并且要提出种种借口。在著名瑞士科学家欧拉（Euler）1770 年发表

的代数著作中，有许多地方用到了虚数。然而，对这种数，他又

加上了这样一个掣肘的评语：“一切形如 −1 ，

− 的数学式，

都是不可能有的、想像的数，因为它们所表示的是负数的平方根。

对于这类数，我们只能断言，它们既不是什么都不是，也不比什么

都不是多些什么，更不比什么都不是少些什么。它们纯属虚幻。”

但是，尽管有这些非难和遁辞，虚数还是迅速成为分数的根

式中无法避免的东西。没有它们，简直可以说寸步难行。

不妨说，虚数构成了实数在镜子里的幻像。而且，正像我们从

基数 1 可得到所有实数一样，我们可以把 −1 作为虚数的基数，

从而得到所有的虚数。 −1 通常写作&i。

不难看出，

− = 9 ×

− = 3&i&，

− = 7 ×

− = 0.246⋅⋅⋅&i&，

等等。这么一来，每一个实数都有自己的虚数搭挡。此外，实数

和虚数还能结合起来，形成单一的表式，例如 5 + −15 = 5 +

15&i&。这种表示方法是卡尔丹发明的，而这种混成的表式通常称

① 验证如下：

（ 5 + −15 ）＋（ 5 − −15 ）＝5＋5＝10

（ 5 + −15 ）×（ 5 − −15 ）

＝（5×5）＋5

− －5

− －（

− × −15 ）

＝25－（－15）＝25＋15＝40。

20&世纪科普经典特藏从一到无穷大

做复数。

虚数闯进数学的领地之后，足足有两个世纪的时间，一直披

着一张神秘的、不可思议的面纱。直到两个业余数学家给虚数作

出了简单的几何解释以后，这张面纱才被揭去。这两个人是：测绘

员威塞-尔（Wessel），挪威人；会计师阿尔刚（Robot Argand），法

国巴黎人。

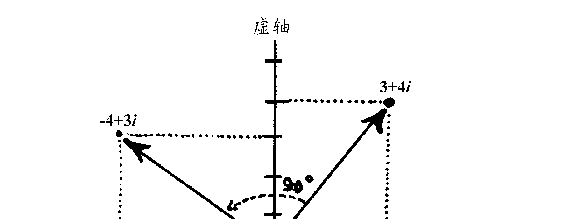
按照他们的解释，一个复数，例如 3＋4&i，可以像图 10 那样表

示出来，其中 3 是水平方向的座标，4 是垂直方向的座标。

所有的实数（正数和负数）都对应于横轴上的点；而纯虚数

则对应于纵轴上的点。当我们把位于横轴上的实数 3 乘以虚数单位

i&时，就得到位于纵轴上的纯虚数 3&i。因此，一个数乘以 i，在几何

上相当于逆时针旋转 90°。（见图 10）。

图 10

如果把 3&i&再乘以&i，则又须再逆转 90°，这一下又回到横轴上，

不过却位于负数那一边了，因为

3&i&×&i&= 3&i&2 = -3，

或

i&2 = -1。

“i&的平方等于 - 1”这个说法比“两次旋转 90°（都逆时针进

第二章

自然数和人工数

行）便变成反向”更容易理解。

这个规则同样适用于复数把 3＋4&i&乘以&i，得到

（3 + 4&i）&i&= 3&i&+ 4&i&2 = 3&i&- 4 = -4 + 3&i。

从图 10 可立即看出，-4 + 3&i&正好相当于 3 + 4&i&这个点绕原点逆时

针旋转了 90°。同样的道理，一个数乘上-&i&就是它绕原点顺时针

旋转 90°。这一点从图 10 也能看出。

如果你现在仍然觉得虚数带有一张神秘的面纱，那么，让我

们通过一个简单的、包含有虚数的实际应用的习题来把这张面纱

揭去吧。

从前，有个富于冒险精神的年轻人，在他曾祖父的遗物中发

现了一张羊皮纸，上面指出了一项宝藏。它是这样写着的：

乘船至北纬、西经&①，即可找到一座荒岛。岛的北

岸有一大片草地。草地上有一株橡树和一株松树&②。还有一座绞

架，那是我们过去用来吊死叛变者的。从绞架走到橡树，并记住

走了多少步；到了橡树向右拐个直角再走这么多步，在这里打个

桩。然后回到绞架那里，朝松树走去，同时记住所走的步数；到

了松树向左拐个直角再走这么多步。在这里也钉个桩。在两个桩

的正当中挖掘，就可找到宝藏。

这道指示很清楚、明白。所以，这位年轻人就租了一条船开往

目的地。他找到这座岛，也找到了橡树和松树，但使他大失所望的

是，绞架不见了。经过长时间的风吹日晒雨淋，绞架已糟烂成土，

一点痕迹也看不出了。

我们这位年轻的冒险家陷入了绝望。在狂乱中，他在地上乱

掘起来。但是，地方太大了，一切只是白费力气。他只好两手空

空、启帆回程。因此，那项宝藏恐怕还在那岛上埋着呢！

这是一个令人伤心的故事。然而，更令人伤心的是：如果这个

① 为不泄密起见，文件上的实际经纬度，已予删去。

② 出于同样的理由，树的种类在这里也改变了，在位于热带地区的宝岛上，显然会有

好多种树的。

20&世纪科普经典特藏从一到无穷大

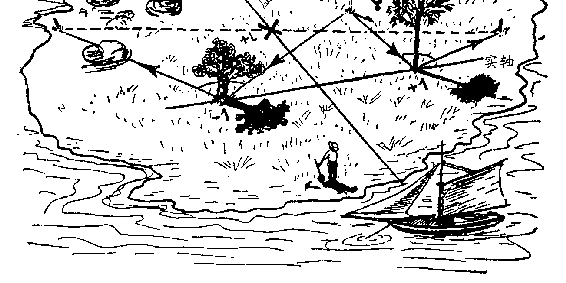
图 11 用虚数来帮我们找宝藏

小伙子懂得点数学，特别是虚数，他本来是有可能找到这宝藏的。

现在我们来为他找找看，尽管已经为时太晚，于他无补了。

我们把这个岛看成一个复数平面。过两棵树干画一轴线（实

轴），过两树中点与实轴垂直作虚轴（见图 11），并以两树距离的

一半作为长度单位。这样，橡树位于实轴上的-1 点上，松树则在

+1 点上。我们不晓得绞架在何处，不妨用大写的希腊字母&Γ（这

个字母的样子倒像个绞架！）表示它的假设位置。这个位置不一定

在两根轴上，因此，&Γ&应该是个复数，即

Γ&=&a + bi

现在来搞点小计算，同时别忘了我们以前讲过的虚数的乘法。既

然绞架在&Γ，橡树在－1，两者的距离和方位便为

-1–&Γ&= -（1 +&Γ）。

第二章

自然数和人工数

同理，绞架与松树相距 1–&Γ。将这两段距离分别顺时针和逆

时针旋转 90°，也就是按上述规则把两个距离分别乘以–&i&和&i。这

样便得出两根桩的位置为：

第一根：(–&i&)[–(1＋&Γ&)] + 1&=&i(&Γ&+ 1) + 1，

第二根：( +&i&)(1–&Γ)－1&=&i(1–&Γ&)–1。

宝藏在两根桩的正中间，因此，我们应该求出上述两个复数

之和的一半，即

1 ［&i(&Γ&+ 1) + 1 +&i(1–&Γ&)–1］

= 1 (&iΓ&+&i&+ 1 +&i–&iΓ–1)&= 1 (2&i)&=&i。

现在可以看出，&Γ&所表示的未知绞架的位置已在运算过程中消

失了。不管这绞架在何处，宝藏都在+&i&这个点上。

瞧，如果我们这位年轻的探险家能做这么一点点数学运算，

他就无须在整个岛上挖来挖去，他只要在图 11 中打×处一挖，就

可以把宝贝弄到手了

如果你还是不相信要找到宝藏，可以完全不知道绞架的位置，

你不妨拿一张纸，画上两棵树的位置，再在不同的地方，假设几次

绞架的位置，然后按羊皮纸文件上的方法去做。不管做多少次，你

一定总是得到复数平面中+&i&那个位置！

依靠-1 的平方根这个虚数，人们还找到了另一个宝藏，这就

是发现普通的三维空间可以和时间结合，从而形成遵从四维几何

学规律的四维空间。下一章在介绍爱因斯坦的思想和他的相对论

时，我们将再讨论这一发现。

在线阅读网：http://wWw.yuedu88.com/

第二章 自然数和人工数

第二章自然数和人工数