第四章 四维世界
一、时间是第四维
关于第四维的概念经常被认为是很神秘、很值得怀疑的。我
们这些只有宽度、厚度和高度的生物,怎么竟敢奢谈什么四维空
间呢?从我们三维的头脑里能想像出四维的情景吗?一个四维的
正方体或四维的球体该是什么样子呢?当我们说的是“想像”一
头鼻里喷火、尾上披鳞的巨龙、或一架设有游泳池并在双翼上有
两个网球场的超级客机时,实际上只不过是在头脑里描绘这些东
西果真突然出现在我们面前时的样子。我们描绘这种图像的背景,
仍然是大家所熟悉的、包括一切普通物体——连同我们本身在内
的三维空间。如果说这就是“想像”这个词的含义,那我们就想
像不了出现在三维空间背景上的四维物体是什么样子了,正如同
我们不可能将一个三维物体压进一个平面那样。不过且慢,我们
确实可以在平面上画出三维物体来,因而在某种意义上可以说是
将一个三维物体压进了平面。然而,这种压法可不是用水压机或
诸如此类的物理力来实现,而是用“几何投影”的方法进行的。
用这两种方法将物体(以马为例)压进平面的差别,可以立即从
图 24 上看出来。
用类比的方法,现在我们可以说,尽管不能把一个四维物体
完完全全“压进”三维空间,但我们能够讨论各种四维物体在三
维空间中的“投影”。不过要记住,四维物体在三维空间中的投影是
立体图形,如同三维物体在平面上的投影是二维图形一样。
为了更好地理解这个问题,让我们先考虑一下,生活在平面
55
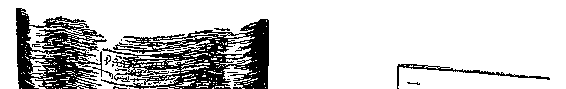
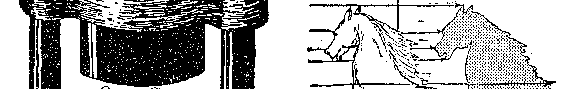
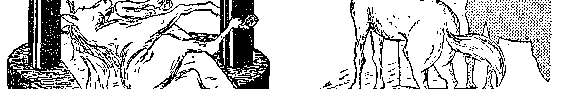
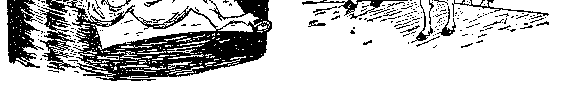
20&世纪科普经典特藏 从一到无穷大
图 24 把一个三维物体“压”进二维平面的两种方法
左图是错误的,右图是正确的
上的二维扁片人是如何领悟三维立方体的概念的。不难想像,作
为三维空间的生物,我们有一个优越之处,即可以从二维空间的
上方、即第三个方向上来观察平面上的世界。将立方体“压”进
平面的唯一的方法,是用图 25 所示的方法将它“投影”到平面
上。旋转这个立方体,可以得到各式各样的投影。观察这些投影,
我们那些二维的扁片朋友就多少能对这个叫做“三维立方体”的神
秘图形的性质形成某些概念。他们不能“跳出”他们那个面像我们
这样看这个立方体。不过仅仅是观看投影,他们也能说出这个东西
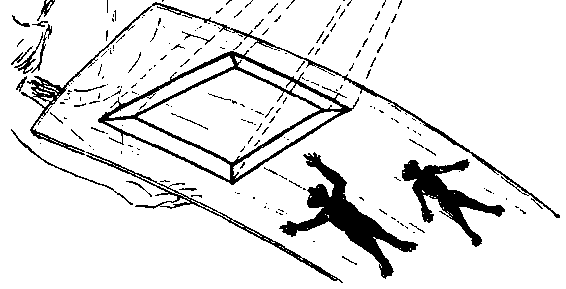
有八个顶点、十二条边等等。现在请看图 26,你将发现,你和那些
只能从平面上捉摸立方体投影的扁片人一样处于困难的境地了。事
实上,图中那一家人如此惊愕地研究着的那个古怪复杂的玩艺儿,
正是一个四维超正方体在我们这个普通三维空间中的投影&①。
仔细端详这个形体,你很容易发现,它与图 25 中令扁片人惊
讶不止的图形具有相同的特征:普通立方体在平面上的投影是两
个正方形,一个套在另一个里面,并且顶点和顶点相连;超正方体
① 更确切地说,图 26 所示的是四维超正方体的三维投影在纸面上的投影。
56


第四章
四 维 世 界
图 25 二维扁片人正惊奇地观察着三维立方体在他们那个世界上的投影
图 26 四维空间的来客!这是一个四维超正方体的正投影
在一般空间中的投影则由两个立方体构成,一个套在另一个里面,
顶点也相连。数一数就知道,这个超正方体共有 16 个顶点、32 条
棱和 24 个面。好一个正方体呀,是吧?
让我们再来看看四维球体该是什么样的。为此,我们最好还
57
20&世纪科普经典特藏 从一到无穷大
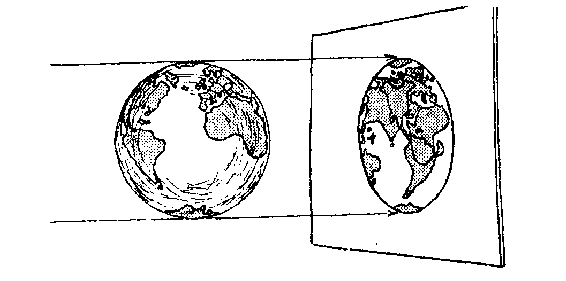
是先看一个较为熟悉的例子,即一个普通圆球在平面上的投影。
不妨设想将一个标出陆地和海洋的透明球投射到一堵白墙上(图
27)。在这个投影上,两个半球当然重叠在一起,而且,从投影上
看,美国的纽约和中国的北京离得很近。但这只是个表面印象。实
图 27 圆球的平面投影
际上,投影上的每一个点都代表球上两个相对的点,而一架从纽
约飞到北京的飞机,其投影则先移动到球体投影的边缘,然后再
一直退回来。尽管从图上看来,两架飞机的航线相重合,但如果它
们“确实”分别在两个半球上飞行,那是不会相撞的。
这就是普通球体平面投影的性质。再发挥一下想像力,我们
就不难判断出四维超球体的三维投影的形状。正如普通圆球的平
面投影是两个相叠(点对点)、只在外面的圆周上连接的圆盘一
样,超球体的三维投影一定是两个互相贯穿并且外表面相连接的
球体。这种特殊结构,我们早在上一章讨论过了,不过那时是作为
与封闭球面相类似的三维封闭空间的例子提出的。因此,这里只
需再补充一句:四维球体的三维投影就是上一节讲到的两个沿整
个外表皮长在一起的苹果。
同样地,用这种类比的方法我们能够解答许多有关四维形
体其他性质的问题。不过,无论如何,我们也决不能够在我们这个
物理空间内“想像”出第四个独立的方向来。
58
第四章
四 维 世 界
但是,只要再多思考一下,你就会意识到,把第四个方向看得
太神秘是毫无必要的。事实上,有一个我们几乎每天都要用的字
眼,可以用来表示、并且也的确就是物理世界的第四个独立的方
向,这个字眼就是“时间”。时间经常和空间一起被用来描绘我们
周围发生的事件。当我们说到宇宙间发生的任何事情时,无论是
说在街上与老朋友邂逅,还是说遥远星体的爆炸,一般都不只说
出它发生在何处,还要说出发生在何时。因此,除表示空间位置的
三个方向要素之外,又增添了一个要素——时间。
再进一步考虑考虑,你还会很容易地意识到,所有的实际物
体都是四维的:三维属于空间,一维属于时间。你所住的房屋就是
在长度上、宽度上、高度上和时间上伸展的。时间的伸展从盖房时
算起,到它最后被烧毁,或被某个拆迁公司扒掉,或因年久而坍塌
为止。
不错,时间这个方向要素与其他三维很不相同。时间间隔是
用钟表量度的:嘀嗒声表示秒,口当口当声表示小时;而空间间隔则是
用尺子量度的。再说,你能用一把尺子来量度长、宽、高,却不能
把这把尺变成一座钟来量度时间;还有,在空间里你能向前、向
后、向上走,然后再返回来;而在时间上却只能从过去到将来,是
退不回来的。不过,即使有上述区别,我们仍然可以将时间作为物
理世界的第四个方向要素,不过,要注意别忘记它与空间不大一
样。
在选择时间作为第四维时,采用本章开头所提到的描绘四维
形体的方法较为便当。还记得四维形体,比如那个超正方体的投
影是多么古怪吧?它居然有 16 个顶点、32 条棱和 24 个面!难怪
图 26 上的那些人会那么瞠目结舌地瞪着这个几何怪物了。
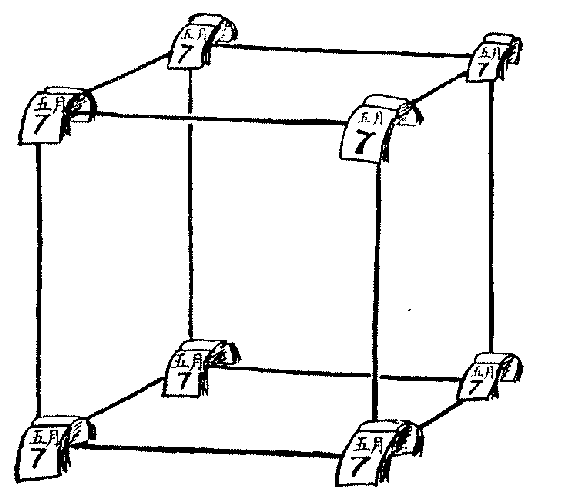
不过,从这个新观点出发,一个四维正方体就只是一个存在
了一段时间的普通立方体。如果你在 5 月 1 日用 12 根铁丝做成一个
立方体,一个月后把它拆掉。那么,这个立方体的每个顶点都应
看做沿时间方向有一个月那么长的一条线。你可以在每个顶点上
59
20&世纪科普经典特藏 从一到无穷大
图 28
挂一本小日历,每天翻过一页以表示时间的进程。
现在要数出四维形体的棱数就容易了(如图 28)。在它开始
存在时有 12 条空间棱,结束时还有这样 12 条&①。另外又有描述各个
顶点存在时间的 8 条“时间棱”。用同样方法可以数出它有 16 个顶
点,5 月 1 日有 8 个空间顶点,6 月 1 日也有 8 个。用同样方法还能
数出面的数目,请读者自己练习数一数。不过要记住,其中有一些
面是这个普通立方体的普通正方形面,而其他的面则是由于原立方
体的棱由 5 月 1 日伸展到 6 月 1 日而形成的“半空间半时间”面。
这里所讲的有关四维立方体的原则,当然可以应用到任何其
他几何体或物体上去,无论它们是活的还是死的。
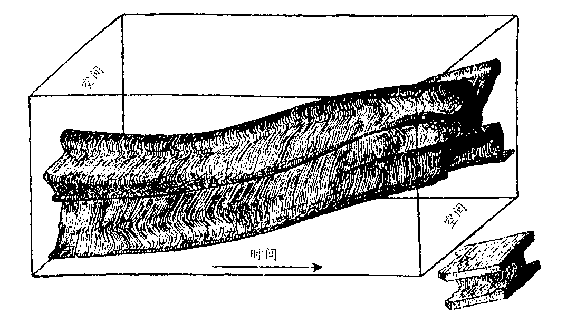
具体地说,你可以把你自己想像成一个四维空间体。这很像
一根长长的橡胶棒,由你出生之日延续到你生命结束之时。遗憾
的是,在纸上无法画出四维的物体来,所以,我们在图 29 上用一
个二维扁片人为例来表现这种想法。这里,我们所取的时间方向
是和扁片人所居住的二维平面垂直的。这幅图只表示出这个扁片
人整个生命中一个很短暂的部分,至于整个过程则要用一根长得
① 如果你不明白这一点,你可以设想有一个正方形,它有四个顶点和四条边。把它沿
与四条边垂直的方向(第三个方向)移动一段等于边长的距离,就又多出四条边了。
60
第四章
四 维 世 界
图 29
多的橡胶棒来表示:以婴儿开始的那一端很细,在很多年里一直
变动着,直到死时才有固定不变的形状(因为死人是不动的),然
后开始分解。
如果想要更准确些,我们应该说,这个四维棒是由为数众多
的一束纤维组成的,每一根纤维是一个单独的原子。在生命过程
中,大多数纤维聚在一起成为一群,只有少数在理发剪指甲时
离去。因为原子是不灭的,人死后,尸体的分解也应考虑为各纤维
丝向各个方向飞去(构成骨骼的原子纤维除外)。
在四维时空几何学的词汇中,这样一根表示每一个单独物质
微粒历史的线叫做“世界线”&*(时空线)。同样,组成一个物体
的一束世界线叫做“世界束”。
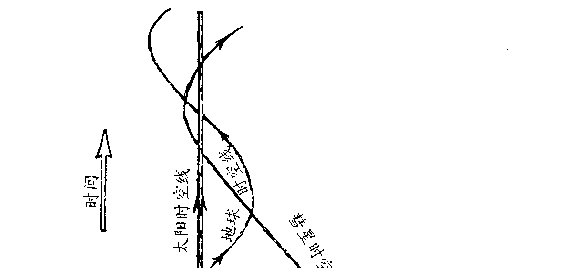
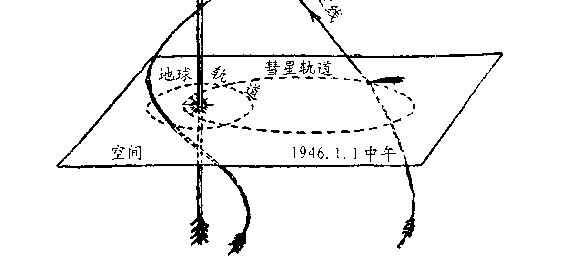
图 30 是一个表示太阳、地球和彗星的世界线&①的天文学例子。
如同前面所举的例子一样,我们让时间轴与二维平面(地球轨道
平面)垂直。太阳的世界线在图中用与时间轴平行的直线表示,
* “世界线”这个名词是本书作者创造和定义的。他去世前不久写的自传,书名就叫
做《我的世界线》。——校者
① 这里原来应说“世界束”较为恰当。不过从天文学角度来看,恒星和行星都可看
做点。
61
20&世纪科普经典特藏 从一到无穷大
图 30
因为我们认为太阳是不动的&①。地球绕太阳运动的轨道近似于圆
形,它的世界线是一条围绕着太阳世界线的螺旋线。彗星的世界
线先靠近太阳的世界线,然后又远离而去。
我们看到,从四维时空几何学的角度着眼,宇宙的历史和拓
扑图形融洽地结合成一体;要研究单个原子、动物或恒星的运动,
都只需考虑一束纠结的世界线就行了。
二、时空当量
要把时间看作和空间的三维多少有些等效的第四维,会碰到
一个相当困难的问题。在量度长、宽、高时,我们可以统统用同一
个单位,如英寸、英尺等。但时间既不能用英寸,也不能用英尺来
量度,这时必须使用完全不同的单位,如分钟或小时。那么,它们
怎样比较呢?如果面临一个四维正方体,它的三个空间尺寸都是 1
① 实际上,太阳相对于其他恒星来说是在运动着的。因此,如果选用星座作为标准,
太阳的世界线将向一个方向倾斜。
62
第四章
四 维 世 界
英尺,那么,应该取多长的时间间隔,才能使四个维相等呢?是 1
秒,还是 1 小时,还是一个月?1 小时比 1 英尺长还是短?
乍一看,这个问题似乎毫无意义。不过,深入想一下。你就会
找到一个比较长度和时间间隔的合理办法。你常听人家说,某人
的住处“搭公共汽车只需 20 分钟”、某某地方“乘火车 5 小时便
可到达”。这里,我们把距离表示成某种交通工具走过这段距离所
需要的时间。
因此,如果大家同意采用某种标准速度,就能用长度单位来表
示时间间隔,反之亦然。很清楚,我们选用来作为时空的基本变换因
子的标准速度,必须具备不受人类主观意志和客观物理环境的影响、
在各种情况下都保持不变这样一个基本的和普遍的本质。物理学中已
知的唯一能满足这种要求的速度是光在真空中的传播速度。尽管人们
通常把这种速度叫做“光速”,但不如说是“物质相互作用的传播速
度”更恰当些,因为任何物体之间的作用力,无论是电的吸引力还是
万有引力,在真空中传播的速度都是相同的。除此之外,我们以后还
会看到,光速是一切物质所能具有的速度的上限,没有什么物体能以
大于光速的速度在空间运动。
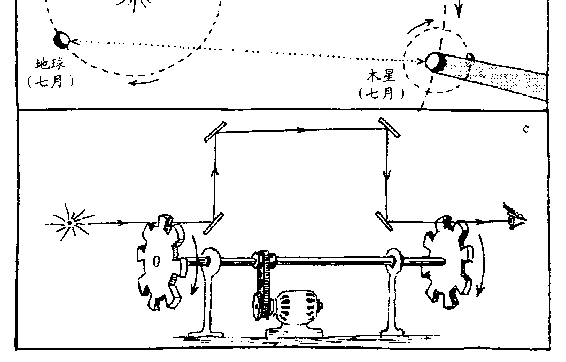
第一次测定光速的尝试是著名的意大利物理学家伽利略(Galileo
Galilei)在 17 世纪进行的。他和他的助手在一个黑沉沉的夜晚到了佛
罗伦萨&*郊外的旷野,随身带着两盏有遮光板的灯,彼此离开几英里
站定。伽利略在某个时刻打开遮光板,让一束光向助手的方向射去
(图 31a)。助手已得到指示,一见到从伽利略那里射来的光,就马上
打开自己那块遮光板。既然光线从伽利略那里到达助手,再从助手那
里折回来都需要一定时间,那么,从伽利略打开遮光板时起,到看到
助手发回的光线,也应有一个时间间隔。实际上,他也确实观察到
一个小间隔,但是,当伽利略让助手站到远一倍的地方再做这个实
验时,间隔却没有增大。显然,光线走得太快了,走几英里路简直
用不了多少时间。至于观察到的那个间隔,事实上是由于伽利略的
* 意大利城市名。——译者
63

20&世纪科普经典特藏 从一到无穷大
图 31
助手没能在见到光线时立即打开遮光板造成的——这在今天称为
反应迟误。
尽管伽利略的这项实验没有导致任何有意义的成果,但他的
另一发现,即木星有卫星,却为后来首次真正测定光速的实验提
供了基础。1675 年,丹麦天文学家雷默(Olaus Roemer)在观察木
星卫星的蚀时,注惫到木星卫星消失在木星阴影里的时间间隔逐
次有所不同,它随木星和地球之间的距离在各次卫星蚀时的不同
64
第四章
四 维 世 界
而变长或变短。雷默当即意识到(你在研究图 31b 以后也会看
出),这种效应不是由于木星的卫星运动得不规则,而是由于当木
星和地球距离不同时,所看到的卫星蚀在路上传播所需要的时间
不同。从他的观测得出,光速大约为 185 000 英里每秒。难怪当初
伽利略用他那套设备测不出来了,因为光线从他的灯传到助手那
里再回来,只需要十万分之几秒的时间啊!
不过,用伽利略这套粗糙的遮光灯所做不到的,后来用更精
密的物理仪器做到了。在图 31c 上,我们看到的是法国物理学家斐
佐(Fizeau)首先采用的短距离测定光速的设备。它的主要部件是
安在同一根轴上的两个齿轮,两个齿轮的安装正好使我们在沿轴
的方向从一头看去时,第一个齿轮的齿对着第二个齿轮的齿缝。
这样,一束很细的光沿平行于轴的方向射出时,无论这套齿轮处
在那个位置上,都不能穿过这套齿轮。现在让这套齿轮系统以高
速转动。从第一个齿轮的齿缝射入的光线,总是需要一些时间才
能达到第二个齿轮。如果在这段时间内,这套齿轮系统恰好转过
半个齿,那么,这束光线就能通过第二个齿轮了。这种情况与汽车
以适当速度沿装有定时红绿灯系统的街道行驶的情况很类似。如
果这套齿轮的转速提高一倍,那么,光线在到达第二个齿轮时,正
好射到转来的齿上,光线就又被挡住了。但转速再提高时,这个齿
又将在光束到达之前转过去,相邻的齿缝恰好在这适当的时刻转
来让光线射过去。因此,注意光线出现和消失(或从消失到出现)
所相应的转速,就能算出光线在两齿轮间传播的速度。为减低所
需的转速,可让光在两齿轮间多走些路程,这可以借助图 31c 所示
的几面镜子来实现。在这个实验中,当齿轮的转速达到 1000 转每
秒时,斐佐从靠近自己的那个齿轮的齿缝间看到了光线。这说明
在这种转速下,光线从这个齿轮到达另一个齿轮时,齿轮的每个
齿刚好转过了半个齿距。因为每个齿轮上有 50 个完全一样的齿,
所以齿距的一半正好是圆周的 1/100,这样,光线走过这段距离的
时间也就是齿轮转一圈所用时间的 1/100。再把光线在两齿间走的路
65
20&世纪科普经典特藏 从一到无穷大
程也考虑进来进行计算,斐佐得到了光速为 300 000 公里每秒或
186 000 英里每秒这个结果,它和雷默考查木星的卫星所得到的结
果差不多。
接着,人们又用各种天文学方法和物理学方法,继两位先驱
之后做了一系列独立的测量。目前,光在真空中的速度(常用字
母&c&表示)的最令人满意的数值是
c&= 299 776 公里/秒
或&c&= 186 300 英里/秒。
在量度天文学上的距离时,数字一般都是非常大的,如果用英
里或公里表示,可能要写满一页纸,这时,用速度极高的光速作为
标准就很便当了。因此,天文学家说某颗星离我们 5“光年”远,
就像我们说某地乘火车需要 5 小时一样。由于 1 年合 31 558 000
秒,1 光年就等于 31 558 000 × 299 776 = 9 460 000 000 000 公里或 5
879 000 000 000 英里。采用“光年”这个词表示距离,实际上已
把时间看作一种尺度,并用时间单位来量度空间了。同样,我们也
可以把这种表示法反过来,得到“光英里”这个名称,意思是指
光线走过 1 英里路程所需的时间。把上述数值代入,得出 1 光英里
等于 0.000 005 4 秒。同样,“1 光英尺”等于 0.000 000 001 1 秒。
这就回答了我们在上一节中提出的那个四维正方体的间题。如果
这个正方体的三个空间尺度都是 1 英尺,那么时间间隔就应该是
0.000 000 001 1 秒。如果一个边长 1 英尺的正方体存在了一个月的
时间,那就应把它看作一根在时间方向上比其他方向长得非常多
的四维棒了。
三、四维空间的距离
在解决了空间轴和时间轴上的单位如何进行比较的问题之后,
我们现在可以问:在四维时空世界中两点间的距离应该如何理解?
要记住,现在每一个点都是空间和时间的结合,它对应于通常所
说的“一个事件”。为了弄清这一点,让我们看看下面的两个事件。
66

第四章
四 维 世 界
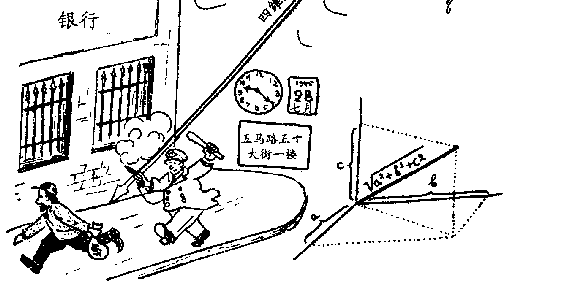
事件I:1945 年 7 月 28 日上午 9 点 21 分,纽约市五马路和第五
十街交叉处一层楼的一家银行被劫。
事件Ⅱ:同一天上午 9 点 36 分,一架军用飞机在雾中撞在纽约第三
十四街和五、六马路之间的帝国大厦第七十九层楼的墙上(图 32)。
图 32
这两个事件,在空间上南北相隔 16 条街,东西相隔半条街,
上下相隔 78 层楼;在时间上相隔 15 分钟。很明显,表达这两个事
件的空间间隔不一定要注意街道的号数和楼的层数,因为我们可
用大家熟知的毕达哥拉斯定理,把两个空间点的坐标距离的平方
和开方,变成一个直接的距离(图 32 右下角)。为此,必须先把
各个数据化成相同的单位,比如说用英尺表达出来。如果相邻两
街南北相距 200 英尺,东西相距 800 英尺,每层楼平均高 12 英尺,
这样,三个坐标距离是南北 3200 英尺,东西 400 英尺,上下 936
67
20&世纪科普经典特藏 从一到无穷大
英尺。用毕达哥拉斯定理可得出两个出事地点之间的直接距离为
2
2
2
3200 + 400 + 936 = 11 280 000 = 3360英尺 。
如果把时间当作第四个坐标的概念确实有实际意义,我们就
能把空间距离 3360 英尺和时间距离 15 分钟结合起来,得出一个表
示两事件的四维距离的数来。
按照爱因斯坦(Albert Einstein)原来的想法,四维时空的距离,
实际上只要把毕达哥拉斯定理进行简单推广便可得到,这个距离在各
个事件的物理关系中所起的作用,比单独的空间距离和时间间隔所起
的作用更为基本。
要把空间和时间结合起来,当然要把各个数据用同一种单位表达
出来,正如街道间隔和楼房高度都用英尺表示一样。前面我们已经看
到,只要用光速作为变换因子,这一点就很容易办到了,这样,15 分
钟的时间间隔就变成 800 000 000 000“光英尺”。如果对毕达哥拉斯
定理作简单的推广,即定义四维距离是四个坐标距离(三个空间的和
一个时间的)的平方和的平方根,我们实际上就取消了空间和时间的
一切区别,承认了空间和时间可以互相转换。
然而,任何人——包括了不起的爱因斯坦在内——也不能把一根
尺子用布遮上,挥动一下魔棒,再念念“时间来,空间去,变”的咒
语,就变出一只亮闪闪的新牌子闹钟来!(图 33)!
因此,我们在使用毕达哥拉斯公式将时空结合成一体时,应该
采用某种不寻常的办法,以便保留它们的某些本质区别。按照爱
因斯坦的看法,在推广的毕达哥拉斯定理的数学表式中,空间距
离与时间间隔的物理区别可以在时间坐标的平方项前加负号来加以
强调。这样,两个事件的四维距离可以表示为三个空间坐标的平方和
减去时间坐标的平方,然后开平方。当然,首先得将时间坐标化成空
间单位。
因此,银行抢劫案和飞机失事案之间的四维距离应该这样计算:
2
2
2
2
3200 + 400 + 936 −800 000 000 000 。
第四项与前三项相比是非常大的,这是因为这个例子取自“日
68
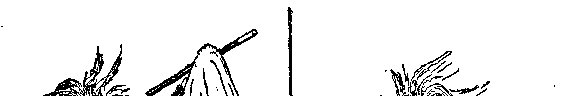



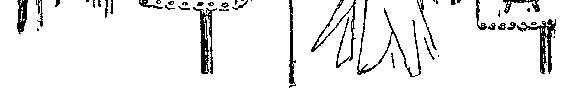
第四章
四 维 世 界
图 33 爱因斯坦教授从来就不会来这一手,但他所做的比这还要强得多
常生活”,而用日常生活的标准来衡量时,时间的合理单位真是太
小了。如果我们所考虑的不是纽约市内发生的两个事件,而用一个
发生在宇宙中的事件作为例子,就能得到大小相当的数字了,比如
说,第一个事件是 1946 年 7 月 1 日上午 9 点整在比基尼岛&*上有一
颗原子弹爆炸,第二个事件是在同一天上午 9 点 10 分有一块陨石落
到火星表面;这样,时间间隔为 540 000 000 000 光英尺,而空间距
离为 650 000 000 000 英尺,两者大小相当。
在这个例子中,两个事件的四维距离是:
( × )2 −( × )2
10
10
10
65 10
54 10
英尺 = 36×10 英尺 ,
在数值上与纯空间距离和纯时间间隔都很不相同了。
当然,大概有人会反对这种似乎不太合理的几何学。为什么对其
中的一个坐标不像对其他三个那样一视同仁呢?千万不要忘记,任何
人为的描绘物理世界的数学系统都必须符合实际情况;如果空间和时
间在它们的四维结合里的表现确实有所不同,那么,四维几何学的定
* 比基尼岛是太平洋西部的一个珊瑚岛。——译者
69
20&世纪科普经典特藏 从一到无穷大
律当然也要按它们的本来面目去塑造。而且,还有一个简单的办法,
可以使爱因斯坦的时空几何公式看来跟学校里所教的古老的欧几里得
几何公式一样美好。这个方子是德国数学家闵可夫斯基(Hermann
Minkovski)提出的,做法是将第四个坐标看作纯虚数。你大概还记得
在本书第二章讲过,一个普通的数字乘以
1
− 就成了一个虚数;我
们还讲过,应用虚数来解几何问题是很方便的。于是,根据闵可夫斯
基的提法,时间这第四个坐标不但要用空间单位表示,并且还要乘以
1
− 。这样,原来那个例子中的四个坐标就成了:
第一坐标:3200 英尺,第二坐标:400 英尺,第三坐标:936 英
尺,第四坐标:8 × 1011&i&光英尺。
现在,我们可以定义四维距离是所有四个坐标距离的平方和的平
方根了,因为虚数的平方总是负数,所以,采用闵可夫斯基坐标的普
通毕达哥拉斯表式在数学上是和采用爱因斯坦坐标时似乎不太合理的
表式等价的。
有一个故事,说的是一个患关节炎的老人,他问自己的健康朋友
是怎样避免这种病的。
回答是:“我这一辈子每天早上都来个冷水浴。”
“噢”前者喊道,“那你是改患了冷水浴病啰!”
如果你不喜欢前面那个似乎患了关节炎的毕达哥拉斯定理,那
么,你不妨把它改成虚时间坐标这种冷水浴病
由于在时空世界里第四个坐标是虚数,就必然会出现两种在物理
上有所不同的四维距离。
在上面那个纽约事件的例子中,两个事件之间的空间距离比时间
间隔小(用同样的单位),毕达哥拉斯定理中根号内的数是负的。因
此,我们所得到的是虚的四维距离;在后一个例子中,时间间隔比空
间距离小,这样,根号内得到的是正数,这自然意味着两个事件之间
存在着实的四维距离。
如上所述,既然空间距离被看作实数,而时间间隔被看作纯虚
数,我们就可以说,实四维距离同普通空间距离的关系比较密切;而
70
第四章
四 维 世 界
虚四维距离则比较接近于时间间隔。在采用闵可夫斯基的术语时,前
一种四维距离称为类空间隔,后一种称为类时间隔。
在下一章里,我们将看到类空间隔可以转变为正规的空间距离,
时距&*也可以转变为正规的时间间隔。然而,这两者一个是实数,一个
是虚数,这个事实就给时空互变造成了不可逾越的障碍,因此,一根
尺子不能变成一座时钟,一座时钟也不能变成一根尺子。
* 此处“时距”当为“类时间隔”。经核对本书中文版修订第一版(2002 年印刷),此
处翻译术语改变,当为校对疏忽,下同。——Ken777 注