例子和原因
亚里士多德在《修辞学》中写道,我们可以在公众辩论中使用举例的方法,而在和哲学家谈话时却不能这么做。同哲学家谈话,必须得提出证据。数学中的一个现象可以表明这两者之间的差别。这个现象就是一条规律:把奇数按顺序加起来,并看一看出现的数字:
这些奇数相加得出的数字是平方数,并且依次排列:
这是不是永远正确呢?我们可以再继续往下算几百次,然后说,行了,我现在有足够例子了。但人们还会不满意,因为只有知道这一规律的原因时,人们才能真正了解其中的奥秘。从这个意义上说,证明一个推论不仅可以使人们了解规律的外部知识,而且还可以更深地了解原因。但不利之处是,求得这样的证明非常麻烦。上面这个例子也不例外。
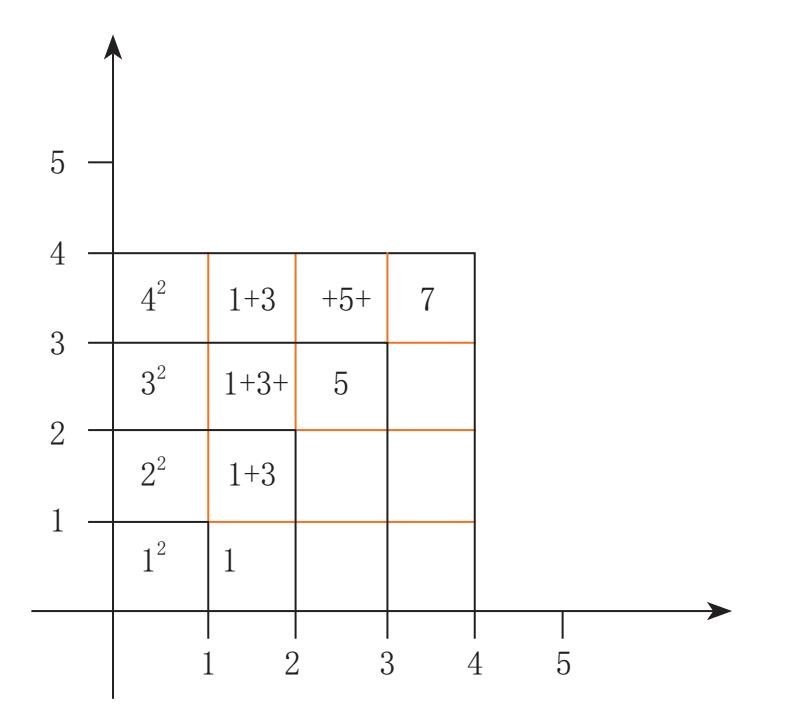
用几何图形可以证明这一例子。我们先来看看等式的右边,即那些平方数。在坐标中,这些平方数以方格的形式体现。接着我们来看坐标,这上面由小方格组成了大方格。和坐标上的1相对应的,只有一个方格,因为12 =1。而22 =4时,方格的数量相当于在原来的基础上增加了三个,也就是1+3=4。以此类推,便可以得出n2 到(n+1)2 是什么情况:纵向增加n小格,横向也增加n小格,如要组成新的方格,则右上角还需要增加一个方格,这样一来总共需要增加2n+1格。这个命题于是就被证实了。
上面这个数列的例子是我在莱布尼茨那里发现的。他在给索菲·夏洛特·冯·汉诺威(1668—1705)的信中讨论了这个例子。莱布尼茨同汉诺威夫人曾有过多年书信往来。可以看出,汉诺威夫人肯定更欣赏哲学家的思维方法,因为宫廷里的证明方法都非常粗暴。汉诺威夫人有一个崇拜者,冯·霍尔斯坦因公爵。有一次,公爵陪同汉诺威夫人游玩。为了给她留下深刻的印象,公爵突然提出要一口气喝光一大杯啤酒,以祝愿夫人身体健康。但表演失败了,那杯啤酒超过了公爵的能力,他不得不把酒都吐出来。而爱情的力量是如此巨大,以至于公爵又试了一次。正如索菲·夏洛特写的那样:“他又狂饮了一次,以证明他对我怀有巨大的热情。”

/南瓜/
在线阅读 网:http://www.Yuedu88.com/