10. 用三个圈告诉你什么是“逻辑”
“这不是很有逻辑么!”要让他人相信那些看来显而易见的事情时,人们常常会这么说。一旦提到逻辑,对方就很少有辩解的可能性。对方就必须同意,情况就是如此。只不过在日常生活中,以逻辑说事的人,常常是错误的,他们说的其实并无逻辑。为了证明这点,当然需要具备一定的认识。
我们常说的“逻辑”一词应该追溯到希腊人。这个词自于希腊语logos,意思就是理性的谈话。很长时间,亚里士多德被看作是逻辑学的奠基人。尽管古希腊时期的其他思想家,如斯多葛派,对逻辑学也做出了自己独特的贡献,但这不能减少亚里士多德的功劳。在《前分析篇》里,他提出了逻辑结论的一个体系。这一体系已有两千多年的历史,这也是科学争论不可动摇的基础。几乎没有其他的思想成就能在这么长时间里享受如此高的荣誉。
一直到二十世纪逻辑才有了新的发展。新的体系被提出,甚至出现了所谓的非经典的逻辑。在这样的逻辑中,古老的逻辑规律已经不再适用。逻辑出现了全面的数学化。极其复杂的新体系是各种技术用途的基础,特别是用在数据处理中。
对哲学讨论来说,除了一些特殊领域,新体系不那么重要。几乎所有情况下,依靠古典逻辑的一些元素就能解决问题。下面我要说说亚里士多德的逻辑。我建议,从一开始就系统地介绍这一体系,因为只有这样,人们才可以看到这一体系的概貌。几个具体例子就可以说明其形式结构。
数学家莱奥哈特·欧拉(1707—1783)早在十八世纪就提出了一种用画面来表示逻辑结构的有用方法。在《给一位德国公主的信》中,他以一种无以伦比的方式说明了亚里士多德的逻辑基础:用画圈的方式来表示逻辑结论。逻辑学家费尽心血要证明的东西,被他变成了画面,从而显示出意义。这是一种基本的简化,下面我会介绍这种简化方法。这种简化方法的内容是什么呢?亚里士多德的逻辑探讨的问题是“如何从已知的命题中得出一种新的命题”,前提是新的命题肯定是从已有的命题中得出的。
命题,一般人们把它理解为一个描述某些东西和主项之间从属关系的句子。一般来说,主项和谓项是概念。它们不仅是指示某个物体,而且还把几个物体归为一个整体。应该提醒一下的是,有些命题不适用这个公式,就是那些与事件有关的命题。例如,在“Esschneit”(下雪了)这个句子中,“es”只是形式上的主项。这就是说,亚里士多德的逻辑基本上是一种简化,但这不是任意的简化,而是一种基于欧洲语言语法的简化。

/莱奥哈特·欧拉/

/月桂饼干/
一种命题肯定或者否定某样东西,例如“每一块月桂饼干都是饼”。这里我们有两个概念:月桂饼干和饼干。两个概念通过这一命题产生了一定的关系,更准确地说,“月桂饼干”是所谓的主项,通过谓项“饼干”得到进一步的说明。
“没有一块月桂饼干是永远不会坏的。”这是一种否定的命题。在这个句子中,主项通过加上一个谓项,也得到了进一步的说明。两种命题是普遍适用的,说明了有关所有月桂饼干的情况。除了普遍的意义外,还具有局部的意义,也就是肯定和否定的意义。例如“有些人喜欢饼干”或“有些人不喜欢甜的东西”的命题。这里不是指所有的人,而是一些人。在日常生活中,“一些人”表示至少两个人。在逻辑学中,数字继续减少,表示至少一个人。
所以,在逻辑学中,人们区别下列四种命题:
所有这些命题都包括两个概念:A和B,人们把这两个概念称为名词的词项。第一个概念,正如上面指出的是主项,主项是进行肯定或否定的主体。第二个概念是谓项,即被肯定或否定的部分。
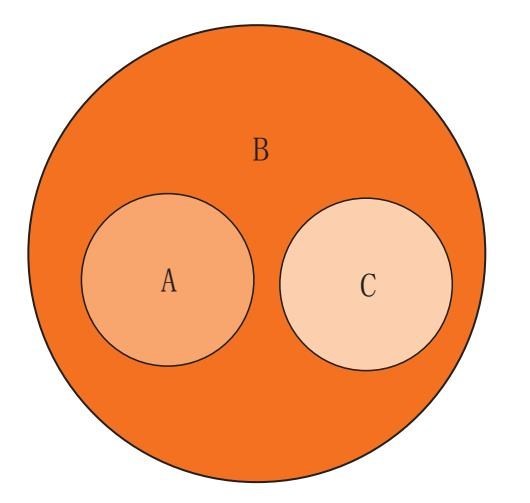
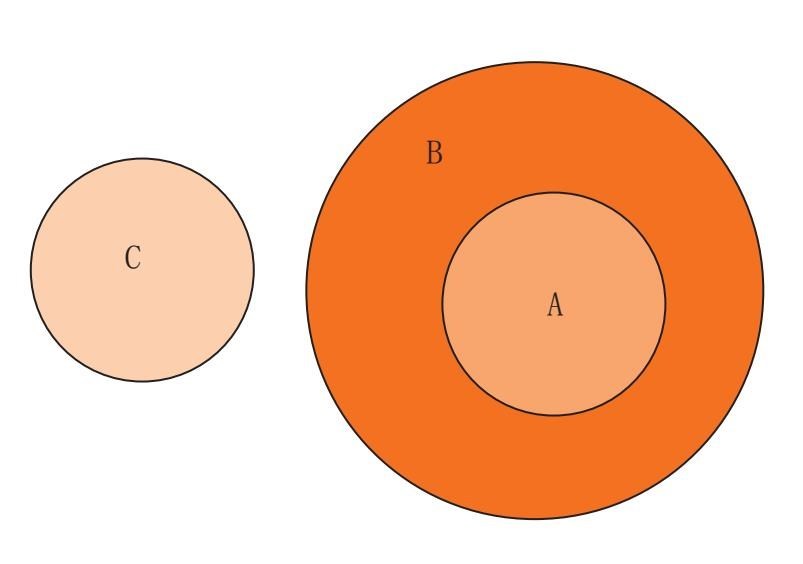
在“饼干是甜的”这个句子里,饼干是主项,甜是谓项。我们可以用简单的圆圈来表示四种命题,从而可以更清楚地看到这些句子的意思。因为像饼干这样一个概念包含无数单个饼干,我们可以把这一概念看作是一个集合,所有的饼干都在这一集合中。我们可以画一个圈,然后说,所有的饼干都在这个圈里,也就是这一集合是一个巨大的饼干盒(有些逻辑学家把这称为是“饼干的宇宙”)。

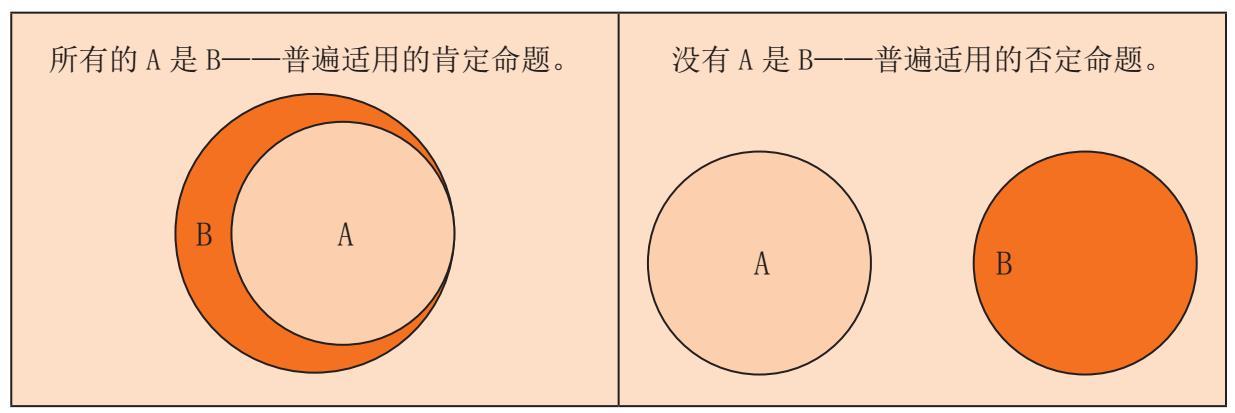
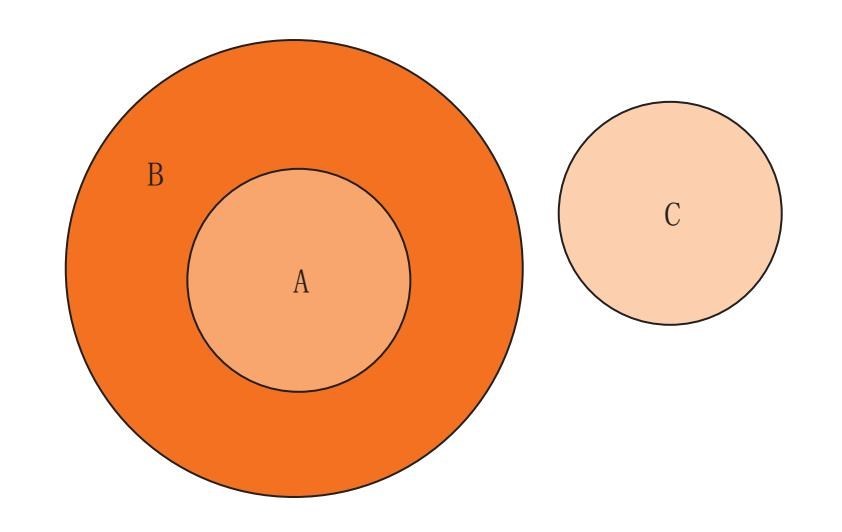
甜的概念是可以类比的,所有甜的东西都包含在里面,不管是饼干、糖块,还是狂欢节吃的糖果。如果我们说“所有饼干都是甜的”,我们可以让第一个圆圈包含在第二个圆圈里。也就是说,在放有所有甜食的盒子里,还有一个饼干盒。
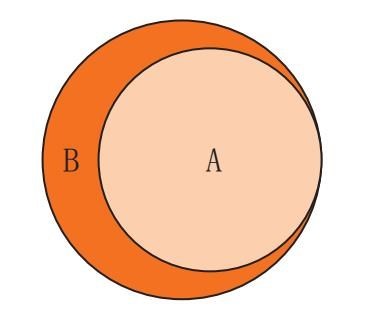
在这里A圈表示主项,B圈是谓项。对普遍的否定命题(没有A是B),例如“没有饼干是不含卡路里的”,可以用下面的图案来表示:
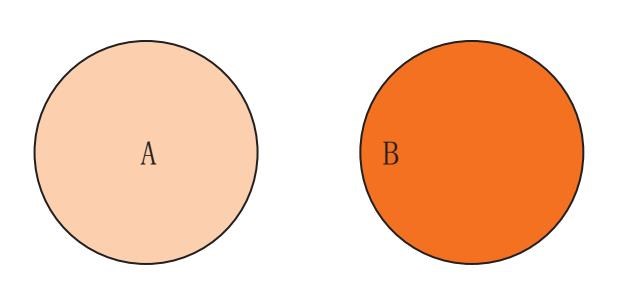
这就是说,饼干盒同不含卡路里的东西的盒子是分开的。一个范畴里的东西没有出现在另一个范畴里,反之亦是如此。分开的圈圈就体现了这点。
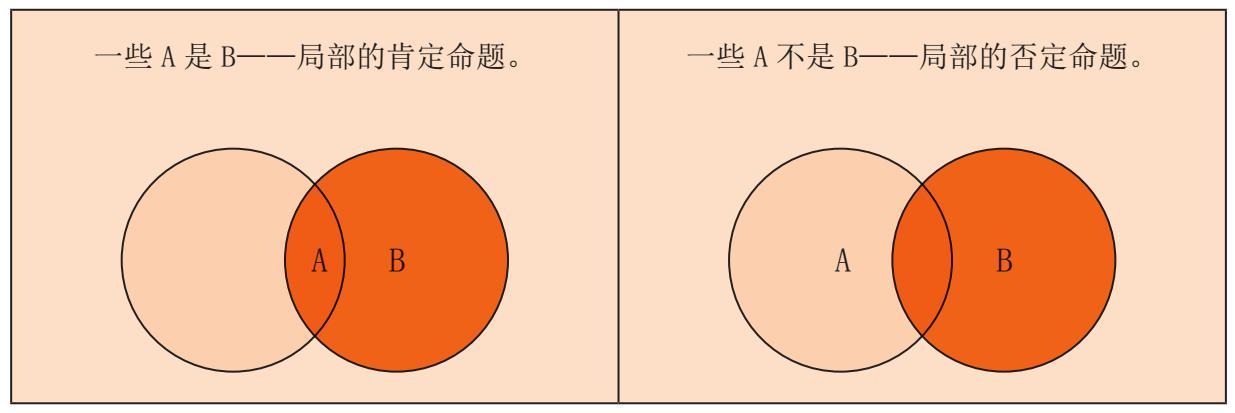
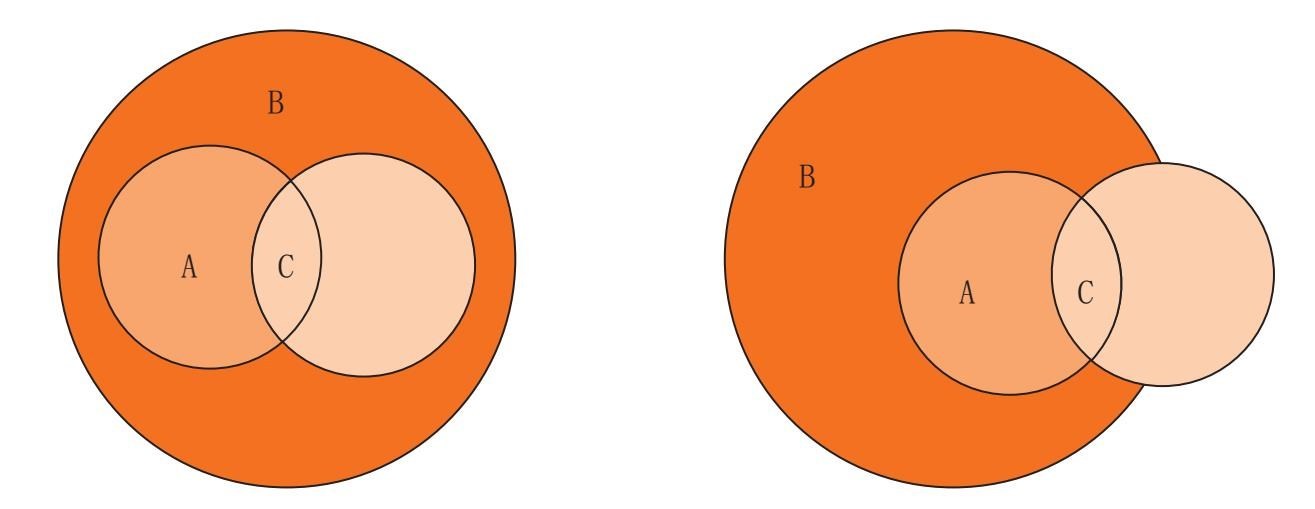
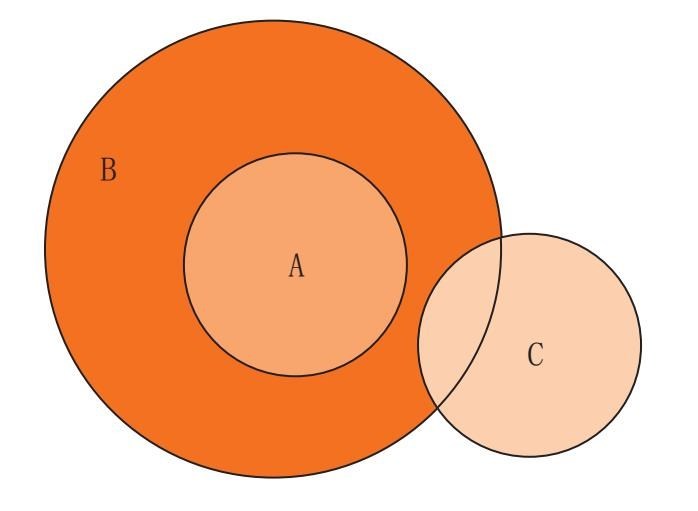
对于局部肯定命题(一些A是B),例如“一些饼干里含有榛子”,圆圈的关系就变成:
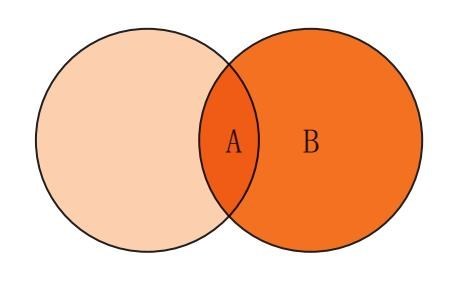
对局部的否定命题(一些A不是B),例如“一些饼干里没有巧克力”,就必须用下列图案来表示:
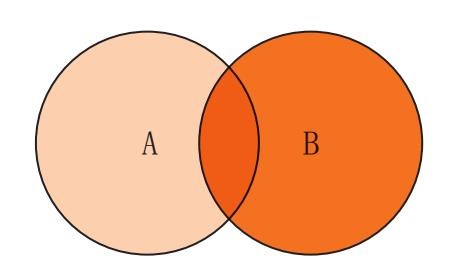
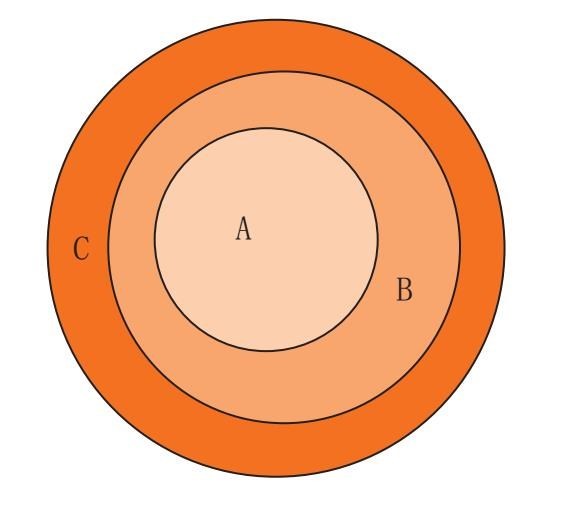
下面是一个概况图,表现了各种盒子之间的关系:
在局部命题中,字母的位置不能任意置换:因为字母的位置表现一个地点,在这个地点上,肯定会出现一个元素。这就是说,我们可以了解所有带有图案的命题。画圈方法的最大优点是,我们可以区分有效逻辑结论和非有效逻辑结论。
我们首先来看一下“所有的A是B”的命题,可以用下面的图示:
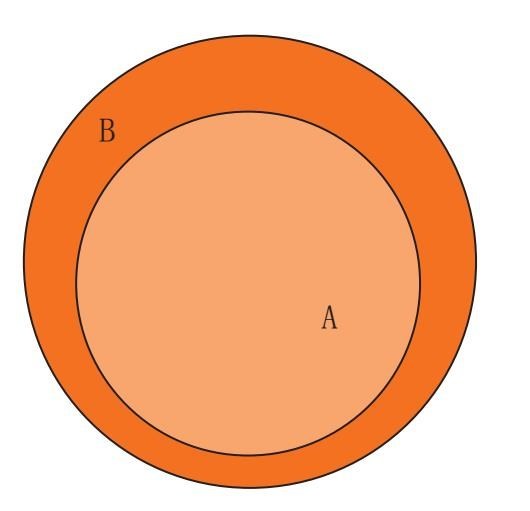
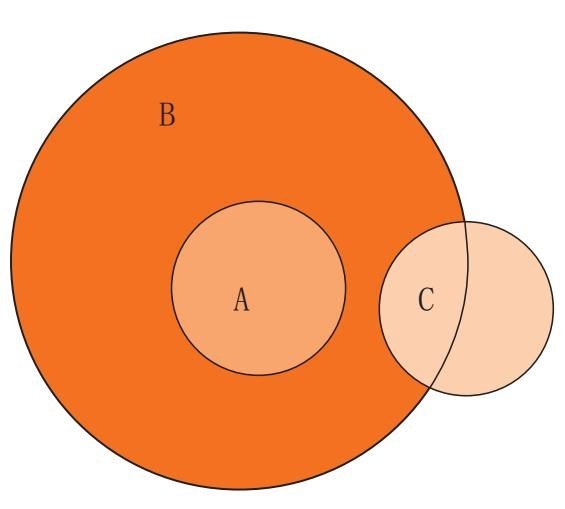
但如果出现了第三个概念,会怎么样?很可能出现这样的情况,即C完全包含在A里:
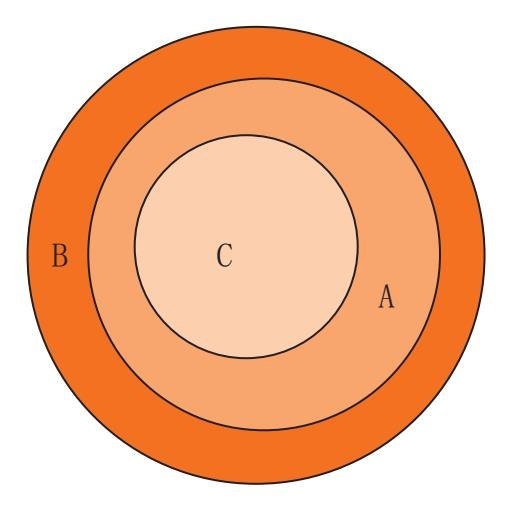
从中就可以得出演绎推理的下列公式(形式上的结论):
最后一个句子是推理。在两个前提中出现的A,被称为是中项,因为它把两个句子连在一起。但在推理中,它并不出现。
如果C仅有一部分属于A,那么这一部分当然也包括在B中,这样就会产生两种可能性。
从中可以得出第二个有效结论:
这样一来,我们又有了一个演绎推理。但如果C完全不在A的位置里,也就是,如果第二个句子是:没有C是A,那会怎么样呢?那样,就会产生三种可能性,首先是:
或者是:
或者是:
这三种可能性都成立。那么可以得出什么样的结论呢?得出的结论是,从B的角度来看,什么结论也得不出来,因为不可能出现任何必然的结果,非常肯定的结果。正因为这样,就无法得出结论,这实际上是一种正常的情况。如果我们非要把这四种命题联系在一起,就会产生至少44 =256种可能性,但大多数的可能性,同我们刚才看到的组合很相似。下面我只集中地讲一下可以得出结果的组合。现在让我们继续思考!如果说,没有C是B的话,在所有的A是B的情况下,可以得出如下结论:
如果C的一部分处于B之外的话,那么这一部分也在A之外,因为A全部在B中。
从中可以得出:
结论:如果C本身包含所有的B,那么一些C也是A。
如果我们是从一个普遍肯定的前提出发,就不可能有其他的可能性。我们可以以相同的方式考虑:如果我们从一个普遍否定的前提出发,或者是一个局部肯定前提或局部否定前提出发,会出现什么样的图案?为了减少篇幅,我在这里只写出结果:
这里还需指出的是,第16种形式同第5种是一样的,只要把C换成A,把A换成C,并以第二种命题来说。这样,实际上就只有19种形式。在需要的情况下,可以使用这些形式。如果一个感兴趣的人问道:“亚历士多德的演绎推理到底有什么用?”我们就能回答道:“亚历士多德的演绎推理是研究四种类型的命题,即普遍肯定的命题、普遍否定的命题、局部肯定的命题和局部否定的命题。在这些命题中,存在着44 =256种组合。从中要筛选出有逻辑结论的组合,这些组合是永远有效的,也就是说不可能出现违背这些组合的例子。而这些组合都可以通过圈圈来表现出来。”
如果提问的人觉得太麻烦了,我们可以提出一些规律来予以说明。根据这些规律,很快就可以判断出什么时候可以得出结论,而什么时候不可以得出结论。
1. 从两个否定的前提中不能得出结论。如果我们说,高卢人不是罗马人,凯尔特人也不是罗马人,我们从中可以知道什么呢?高卢人是凯尔特人还是不是?从这些信息中得不出任何结论。
2. 不能从两个局部命题中得出结论。如果说,一些狗四处乱串,一些狗长虱子。从这两个信息中得出一个可靠的结论吗?当然,乱窜的狗会长虱子,这有可能,但绝非此不可。
下面还有三个规律,这些规律虽然不是很清晰,但仍然有效:
3. 如果前提中的一个是否定的,结论就一定是局部的。
4. 如果前提中的一个是局部的,结论也一定是局部的。
5. 如果两个前提都是肯定的,结论也是肯定的。但要注意:即使两个前提都具有普遍性,但结论不一定非具普遍性不可。
另一个重要问题与名称有关。我们在上面得出的结论都是从名称上得出的,这些名称从一开始就指复数的形式,例如“饼干”,“月桂饼干”。换句话说,就是命题的主项和谓项都是概念。
但如果我们的命题是指单一的东西,情况会如何呢?
如果我们说:我现在给你的这块饼干,是月桂饼干。
乍看这是一个局部命题,因为这里指的是一块饼干。如果只有一块的话,那么它要比一部分还要少,所以是不是要把这一命题看作是非常局部的呢?尽管这一命题猛一眼看上去非常令人信服,但还是错误的。因为“我给你的这块饼干”看起来似乎很少,但这里的饼干指的还是所有的饼干。
事实上,一个单数的命题,哪怕一个只牵涉到一样东西,都必须被当作普遍的东西来对待。这一规律使我们能把普遍命题的所有演绎推理都扩展到单数的命题,从而就提高了逻辑学的实际用途。
在线阅读:http://www.yuEdu88.com/