继续思考和变换思考
科学文章中的思想实验有一种奇怪的诱惑力,思想实验是叙述性的,而别的实验都是求证、进行区别或组合,所以我们就更应该学习如何批判地对待思想实验。
我们再来看上面提到的第一个例子:“想象一下,现在打仗了,可没有人去。”我上面说明了,和平运动人士在什么样的条件下使用了这一口号。真要这么做,全面的拒绝参战会使战争消失,实现和平。这是一个具有说服力的结论。但这个说法有什么漏洞吗?我们可以通过改变思想实验,来检查这一实验是否有效。那些反对和平主义的人就是这么做的。他们指出,如果我们从理想化的情况,即没有人去打仗,过渡到更现实的情况,即有一些喜欢打仗的人上战场了,这一前提的变化就会动摇整个想法。在大规模杀伤性武器存在的今天,一些人参战就足以使其他人遭受战争的苦难。极少的人就能引发战争,我们只要想一想那些恐怖行为,就会认可这一看法。把思想实验稍微改动一下,就会发现这一思想实验的弱点。
此外,我们也可以证明,布莱希特——大家习惯认为这句话出自于他之口——实际上根本就不认为人们应该避免战争。相反,他是一个竭力主张斗争和战争的人,对反战人士他也没说什么好话。我们只要看一下这一名句在它原来的上下文究竟是什么意思,就会恍然大悟。这个句子可以在布莱希特的一个非正规的出版物里找到,它在二十世纪六十年代由一个匿名出版人出版。出版人把“想象一下,现在打仗了,可没有人去”这句话放在了布莱希特的一首诗歌前面。在原来的版本中,这首诗是这样的:
我们清楚地看到,受到谴责的不是去打仗的人,而是那些留在家里的人。所以,这一思想实验在布莱希特那里不是展示和平的愿景,而是提出可怕的警告。
下面还有一个例子。这里我又会回到“永恒”这个主题。但这次涉及的不是长生不老,而是一样东西不断地轮回。人尽管会死,但过了一段时间后又会重新回到人间。人不知什么时候会再次出生,然后成长、工作和生活,然后接着死去、重生……这真是一个奇特的想法。在东方的宗教里,这个想法非常普遍。在西方,这一想法受到尼采(1844—1900)的追捧。在尼采看来,同样的东西不断地轮回,不是一种奇怪的念头,而是可以被证实的。下面就是他在1888年早些时候提出的大胆设想:
(《权力意志》,尼采著,孙周兴译,商务印书馆,2007)
尼采认为这是“至高”的想法,并相信它也具有道德意义,因为人们在做所有的事情时,都必须问一下自己:“你只想做一次,还是无数次?”很明显,没有许多东西可以通过这个测试。
上面是尼采的例子。我们要怎样用批判的眼光来看待他的思想实验呢?首先是要质疑他的先决条件。时间真的是无穷无尽的吗?有没有一种可以被确定的世界状态?世界真的像尼采所提出的那样有边际吗?几乎所有的先决条件都十分可疑,所以我们可以不慌不忙地说,你的证明很不错,只是先决条件都不对。
我们也可以用其他方式来看待思想实验,即把它引入一个模型中并看一看,这一思想实验是否达到预期的效果。我们来举一个特殊的例子。
哲学家西美尔(1858—1918)想出了一个模型,尼采的理论在这个模型中很难成立。这是一个非常简单的模型,它不牵涉重大历史事件,但需要一些数学知识。西美尔设计了一种机械过程:三个自转的轮子,也可以说是永恒轮回的轮子。从这个意义上来说,这个例子很合适。再说,尼采自己也是从自然科学的论点出发的,采用一个机械过程来反证他的观点也很合适。
我们来想象一下,三个大小完全一样的轮子,它们都围绕同一个轴转。我们在三个轮子上各画一个点,并使三个点在一条直线上。然后我们推动轮子,第二个轮子的速度是第一个轮子的一倍;第三个轮子的任务就是要动摇尼采的思想实验,这一轮子的旋转速度为1/π(π=3.14159265……)。并且这些轮子能无止境地转下去。没有摩擦的情况下,什么时候三个点又会回到同一条线上?换句话说就是,什么时候会出现轮回?

/尼采/
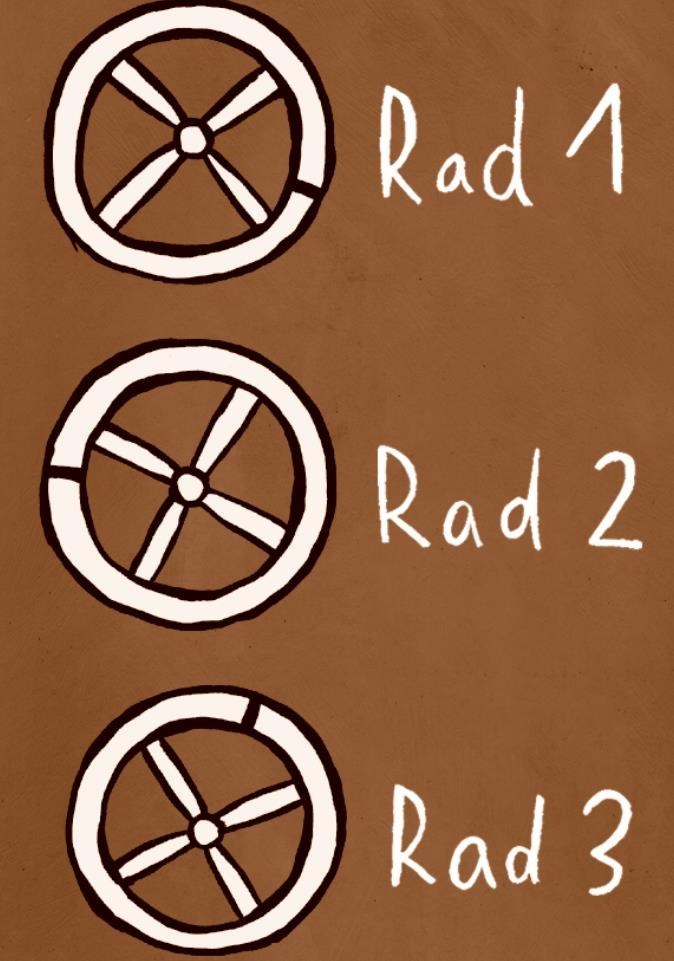
/轮子1/轮子2/轮子3/
我们看到第二个轮子旋转速度是第一个轮子的一倍,转两圈后,这两个轮子上的点又回到同一条线上了。再一下次出现这种情况是转四圈之后,以此类推。同一东西的轮回有了保证,尼采胜利了!但是,第三个轮子却制造了很多麻烦。它的旋转速度是多少呢?对了:第一个轮子围绕着轴心转一圈后,第三个轮子应该是转了1/π圈。那么,第一个轮子转了两圈后,第三个轮子应该转了2/π圈。如果π正好等于3的话,在第一个轮子转了三圈后,这两点就在一条线上了。不幸的是,π是一个无理数,小数点后有一连串无穷无尽的数字,没有人可以得出最后的结果:π=3.14159265……
无止境的数字π看起来是无害的,但它的一口气比尼采的“永恒”还要长。1/π,2/π,3/π……没有一个能成为整数,但我们又必须求得整数,因为只有这样,三个轮子上的三个点才能重新在一条线上。
从中可以得出什么结论呢?这说明至少有一种世界状态用数学证明是不能重复的。三个轮子上的点不能相遇,尼采的证明也随之失去了说服力。轮子尚且如此,比轮子复杂得多的历史事件又怎么能重复呢?
在 线阅DU网:http://Www.yuedu88.com/